课程内容来源:https://tai-e.pascal-lab.net/
实验作业的实现:https://github.com/Ling-Yuchen/Tai-e-assignments/
部分实验作业思路参考:https://vgalaxy.gitee.io/2022/05/05/static-analysis/
01 - Introduction
1. 静态分析:运行前对程序进行分析
是否存在私有信息泄露?
是否存在空指针异常?
是否存在强制类型转换异常?
是否允许存在指向同一内存块的指针?
是否存在 fail 的 assert 语句?
是否存在可以删除的死代码?
……
2. 莱斯定理(Rice’s Theorem)
Any non-trivial property of the behavior of programs in a r.e. language is undecidable.
通俗来讲就是,以平时常用的编程语言写的程序,对于其有用的动态运行时性质,无法做出准确判断
——不存在完美的(sound & complete)静态分析
对 soundness 妥协:产生漏报(false negatives)(可以接受)
对 completeness 妥协:产生误报(false positives)(不希望发生)
静态分析:在确保 soundness 的前提下,在分析的准确度和速度之间做出有效的平衡
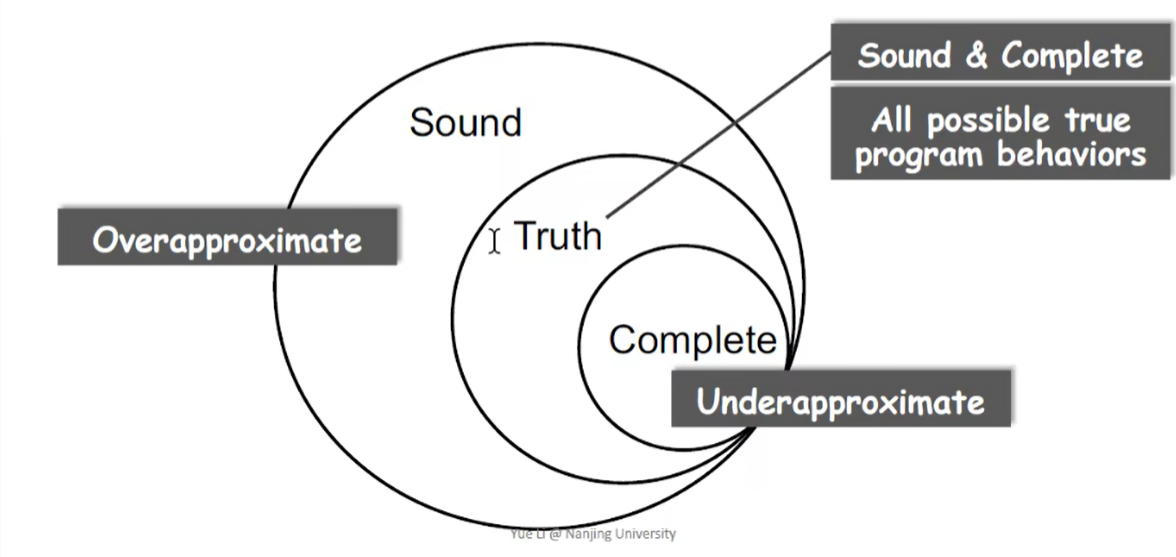
3. 静态分析技术:抽象+近似
抽象(abstraction):把具体域的值映射到抽象域的值
近似(Over-approximation):在抽象层面定义转移函数;由于无法枚举所有路径,所以使用 flow merging 处理 control flow
本节重点
- 静态分析与(动态)测试的区别?
- 理解 soundness, completeness, false negatives 和 false positives 的概念
- 为什么静态分析需要保证 soundness?
- 怎样理解 abstraction 和 over-approximation?
02 - Intermediate Representation
1. 编译器(Compiler)与静态分析(Static Analysis)
编译器:源码 =>(词法分析器 Scanner)=> Tokens =>(语法分析器 Parser)=> AST =>(类型检查 Type Checker)=> Decorated AST =>(Translator)=> IR =>(Code Generator)=> 机器码
静态分析需要在编译器前端生成的 IR 的基础上进行,e.g. 代码优化
2. 抽象语法树(AST) vs. 中间表示(IR)
抽象语法树:贴近语法结构;依赖于不同语言;适合做快速的类型检查;缺少控制流信息
中间表示:贴近机器码;具有语言无关性;简洁而统一;包含控制流信息;通常作为静态分析的基础
3. 中间表示(三地址码)
右侧最多只有一个操作符;每种指令都有对应的三地址码
- x = y bop z
- x = uop y
- x = y
- goto L
- if x goto L
- if x rop y goto L
4. 真实的静态分析器中的三地址码:Soot’s IP
关于 JVM 的补充:
invoke-special: call constructor,call superclass methods,call private methods
invoke-virtual: call instance methods(virtual dispatch)
invoke-interface: cannot optimize,checking interface implementation
invoke-static: call static methods
method signature: class name,return type,method name,parameter type
5. 控制流分析
输入三地址码,输出控制流图
Basic Block 定义:有且仅有一个入口和一个出口的指令块
确定 Basic Block 的算法:
- 第一条指令是基本块的入口
- 所有跳转的目标指令是基本块的入口
- 所有跳转指令的下一条指令是基本块的入口
- 从一个入口指令到下一条入口指令的前一条指令构成一个基本块
控制流图:
节点为基本块(basic blocks)
一条从基本块A到基本块B的边表示,存在从A尾部到B首部的有条件或无条件跳转,或者顺序上B紧跟着A且A的最后一条指令不是无条件跳转
加上 Entry 和 Exit 表示程序的入口和出口(类似哨兵节点)
本节重点
- 编译器和静态分析器之间的关系?
- 理解三地址码及其通常的形式(in IR Jimple)
- 怎样在 IR 的基础上构建 basic blocks?
- 怎样在 basic blocks 的基础上构建控制流图?
03 - Data Flow Analysis(Application)
1. 数据流分析概览
How application-specific Data(abstraction) Flows(safe-approximation) through the Nodes (Transfer function)and Edges(Control-flow handling) of CFG?
may analysis:输出信息可能是正确的(over-approximation)
must analysis:输出信息必须是正确的(under-approximation)
2. 数据流分析前驱知识
Input and Output States
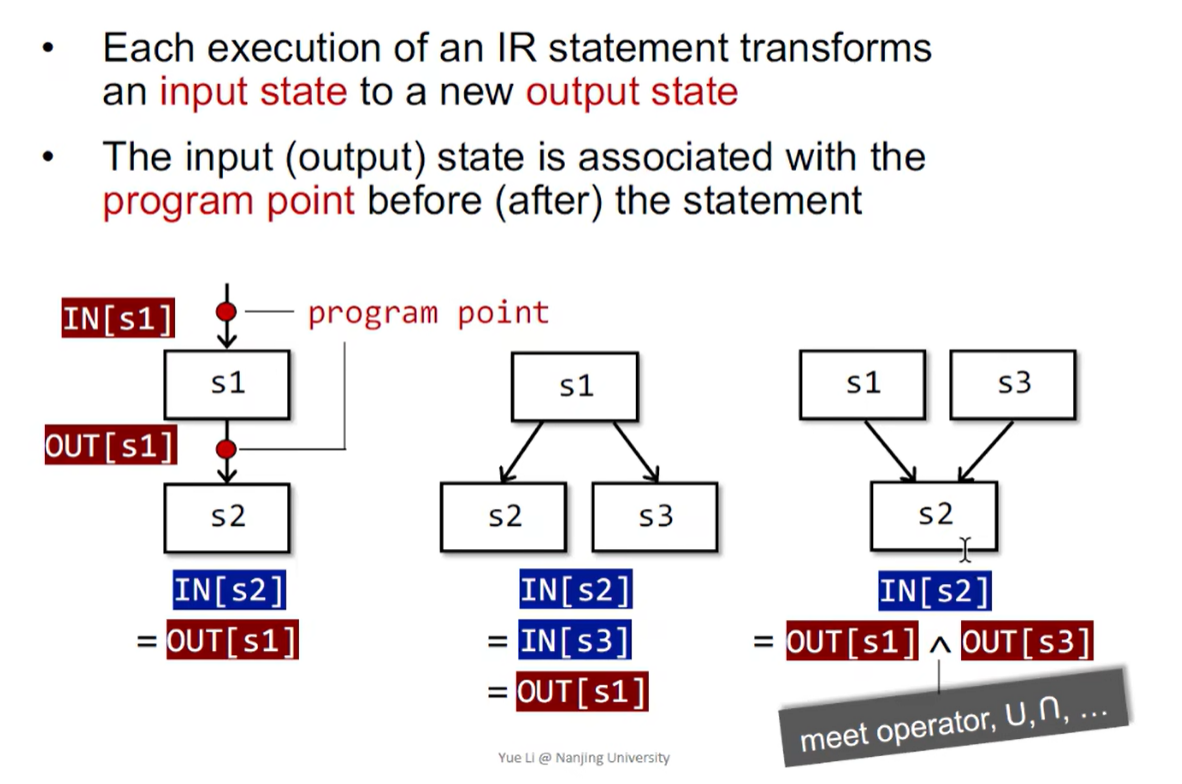
在数据流分析应用中,将每一个 program point 与一个 表示该点所有观测到的 program states 的集合的抽象的数据流值(data-flow value) 联系起来
数据流分析是对所有的语句,通过解析 safe-approximation 的约束规则,得到一个 solution(给每个 program point 一个 data-flow value)
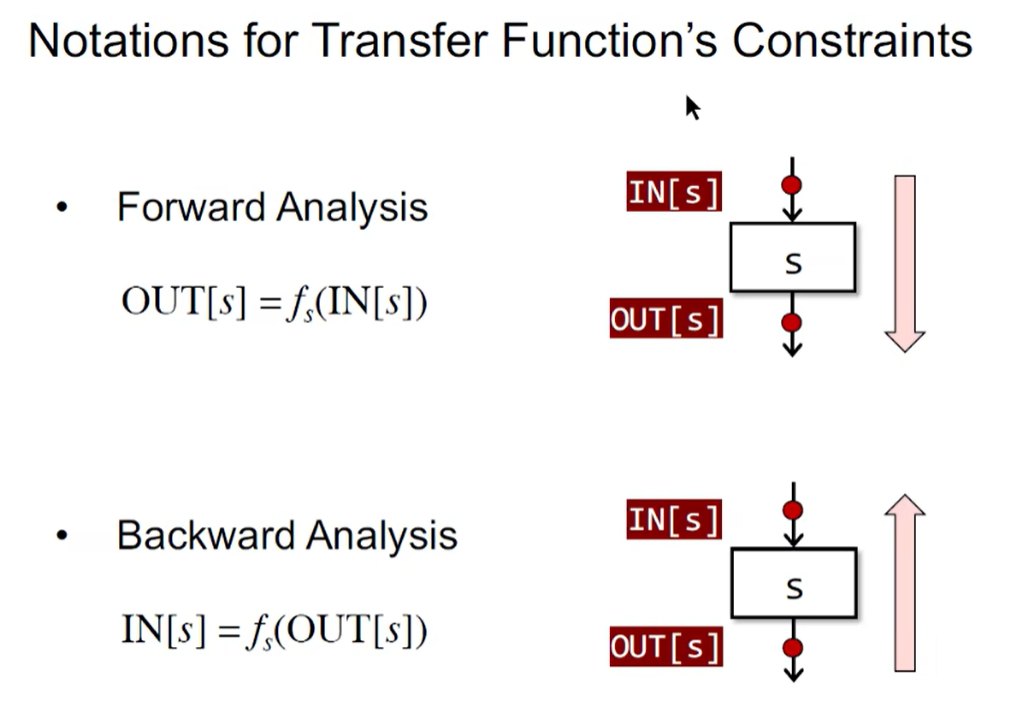
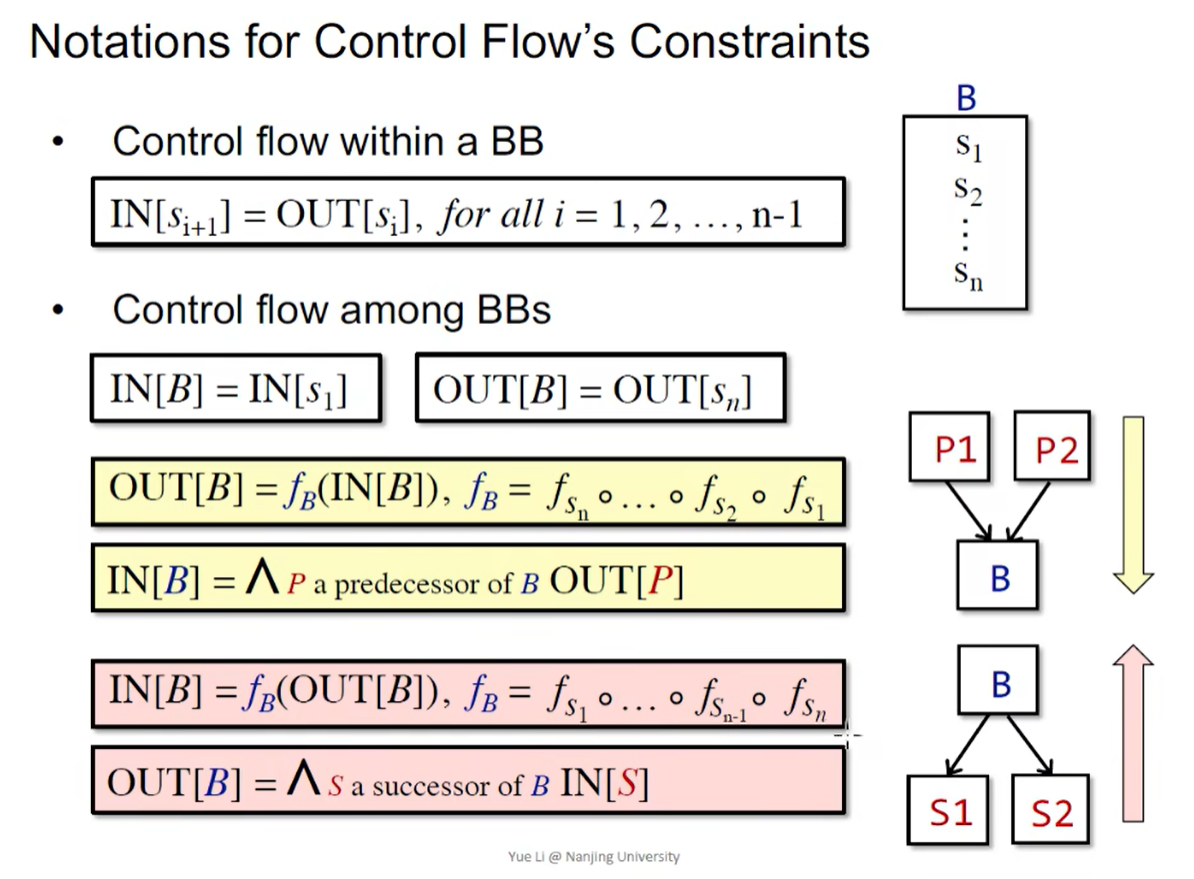
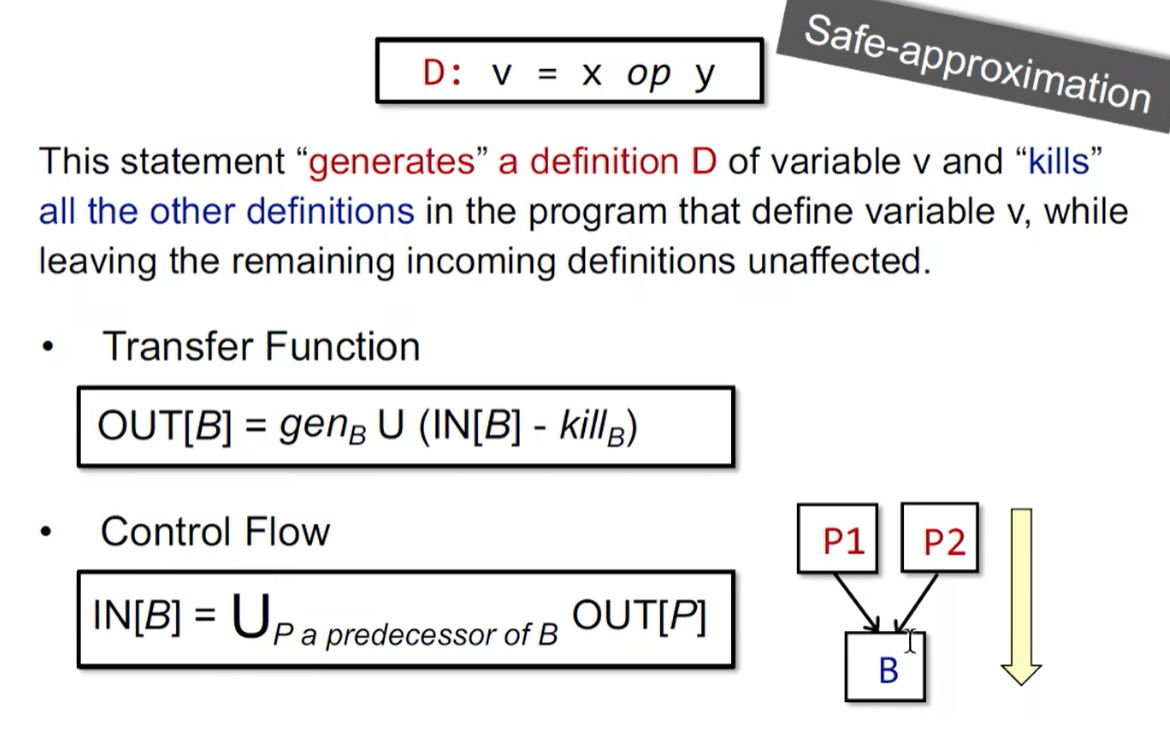
3. 定义可达性分析(Reaching Definition Analysis)
定义可达性:A definition d at program point p reaches a point q if there is a path from p to q such that d is not killed along the path.
定义可达性可以用于 侦测可能的未定义的变量
理解定义可达性分析:
用一个比特表示某个变量在某一点的定义可达性
用一个 n 维比特向量表示 n 个变量在某一点的定义可达性
定义可达性分析算法:
注意:
在算法模板中边界条件(OUT[entry])单独初始化
对于 OUT[B],may analysis 一般初始化为空;must analysis 一般初始化为 top

为什么该迭代算法最终会停下来?
对于 Transfer Function,OUT[S] 只受 IN[S] 的影响,当个更多的 facts 流入 IN[S] 时,要么被 kill 要么存活下来并永远被保留,故 OUT[S] 永远不会缩减(e.g. 0 => 1 或 1 => 1),又因为定义的变量数量是有限的,故该迭代一定会停下来(实际上到达了一个不动点)
4. 活跃变量分析(Live Variable Analysis)
Live variable analysis tells whether the value of variable v at program point p could be used along some path in CFG starting at p(AND v should not be redefined before usage). If so, v is live at p. Otherwise, v is dead at p.
活跃变量信息可用于寄存器分配(倾向于使用存有 dead value 的寄存器来存新数据)
理解活跃变量分析:
用一个比特表示某个变量在某一点是否活跃
用一个 n 维比特向量表示 n 个变量在某一点是否活跃
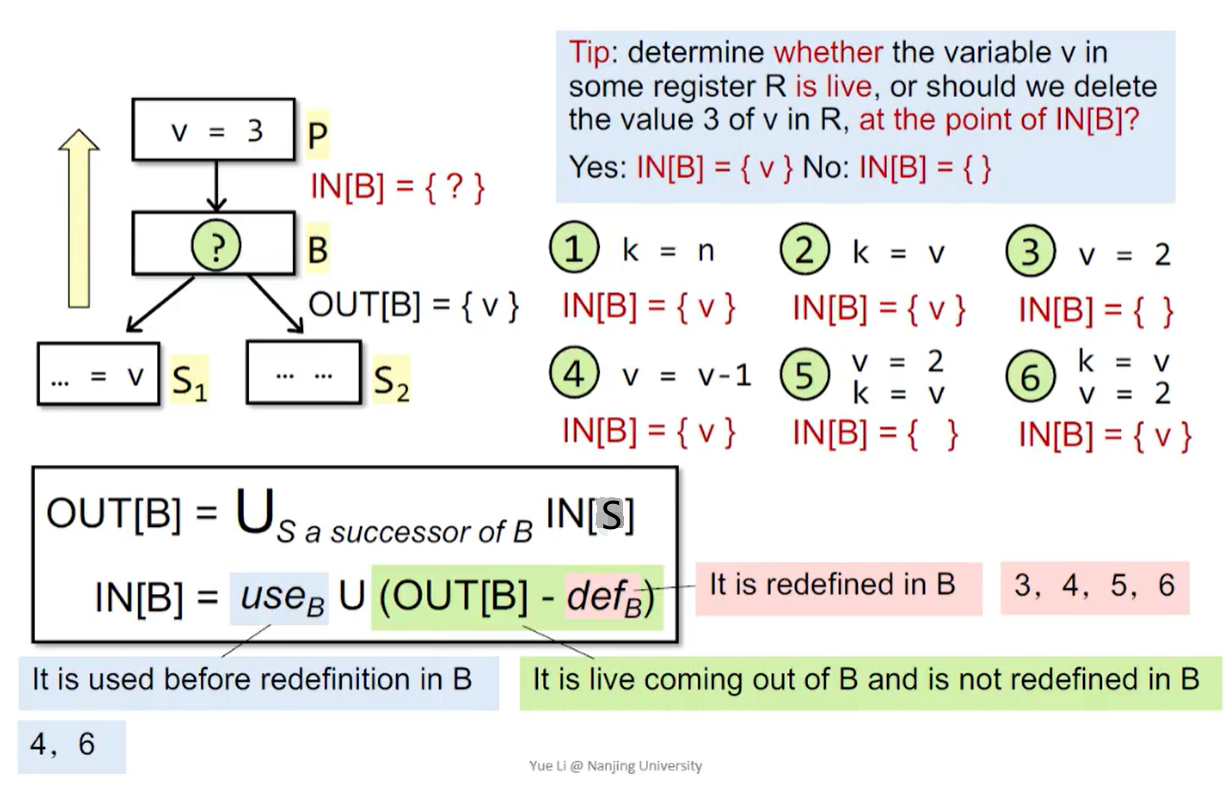
注意 use 的定义为:在重定义之前被使用
活跃变量分析算法:
注意:
在算法模板中边界条件(IN[entry])单独初始化
对于 IN[B],may analysis 一般初始化为空;must analysis 一般初始化为 top

5. 可用表达式分析(Available Expressions Analysis)
一个表达式,形如 x op y,在某个 program point p 是可用的,需要满足:
- 从 ENTRY 到 p 的所有路径都必须计算过 x op y 的值
- 在这些路径各自最后一次计算该表达式的值之后没有修改过 x 或 y 的值
理解可用表达式分析:
用一个比特表示某个表达式在某点是否可用
用一个 n 维比特向量表示 n 个表达式在某点是否可用
注意这是一个 must analysis

可用表达式分析算法:
注意在 must analysis 中的初始化方式

6. 不同数据流分析应用的对比
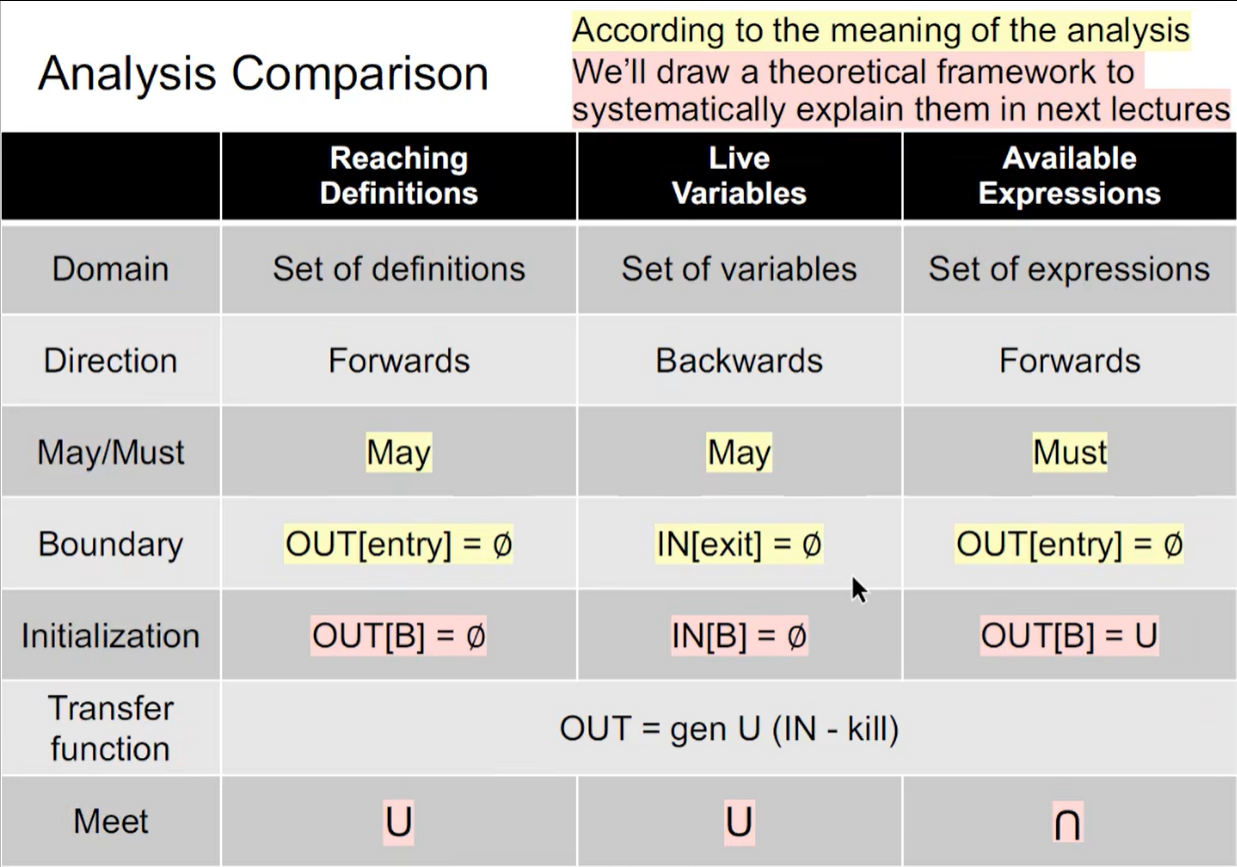
本节重点
- 理解三种数据流分析
- 能说出三种数据流分析的相似与不同
- 理解迭代算法为什么最终能停下来
04 - Data Flow Analysis(Foundations)
1. 从另一个角度来看迭代算法
假设给定的 CFG 有 k 个节点,迭代算法每次迭代更新每个节点的 OUT[n]
定义 k-tuple (OUT[n1], … , OUT[nk]),则该元组为集合 V^k 的一个元素(V 是数据流分析的值的域)
那么每次迭代可以视作作用了转移函数和流控制处理的一次映射,即:F: V^k —> V^k
整个算法就是在不断地输出这样的 k-tuple 直到出现连续两个相同的为止
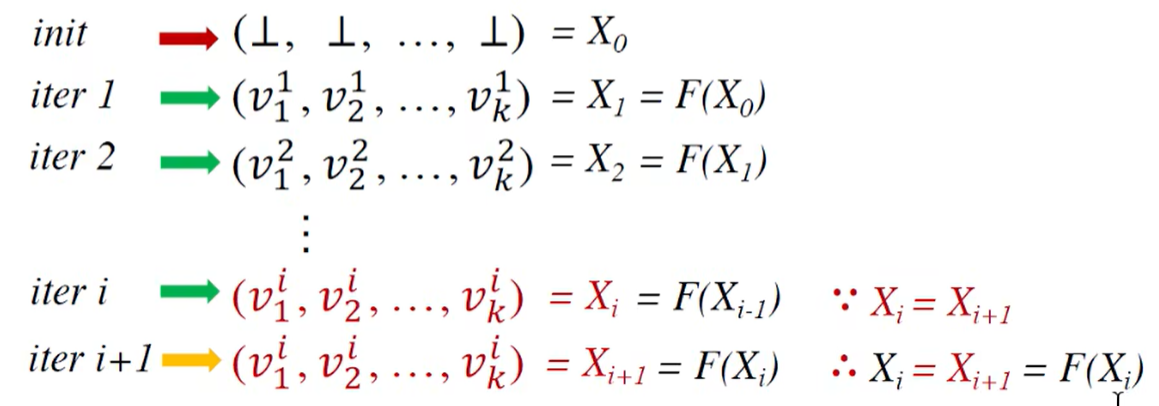
迭代算法会在 X = F(X) 处停下来,即数学定义上的一个不动点(fixed point)
思考:
- 算法能保证到达不动点吗?
- 如果能,那么只有一个不动点吗?若超过一个不动点,那么我们能到达最优解的不动点吗?
- 算法要多久才能到达不动点?(时间复杂度)
2. 偏序
偏序关系(Partial Order)满足自反性、反对称性、传递性
一个偏序集(poset)中的任意两个元素之间不一定满足偏序关系
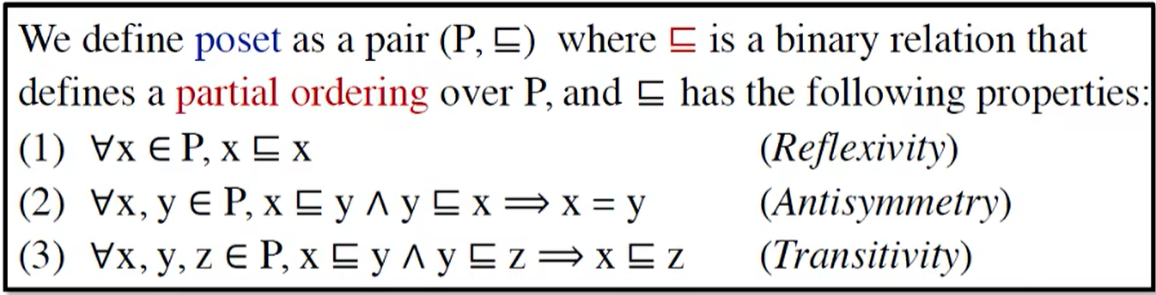
3. 上界和下界
上界(upper bound)和下界(lower bound)
最小上界(least upper bound)和最大下界(greatest lower bound)

最小上界(least upper bound)和最大下界(greatest lower bound)

不是每个偏序集都有最小上界(最大下界);若偏序集存在最小上界(最大下界),则是唯一的
4. 格、半格、全格、格的积
格(Lattice)
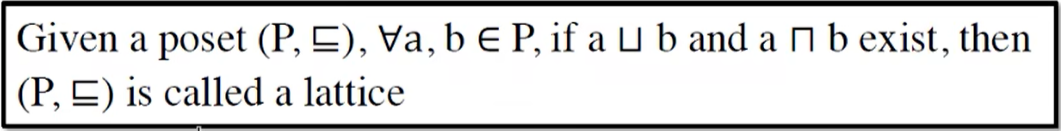
半格(Semilattice)

全格(Complete Lattice)


有穷格一定是全格,全格不一定是有穷格
格的积(Product Lattice)

5. 通过格来表达数据流分析框架
数据流分析框架(D, L, F):
- D:数据流的方向(forward 或 backward)
- L:一个包含分析域(domain)以及 join 和 meet 操作的格
- F:一组定义在在域(domain)上的转移函数(transfer function)
数据流分析可以视作:对格的值迭代地作用转移函数(transfer function)和 join 或 meet 操作
6. 单调性与不动点定理

证明:不动点存在且是最小(大)的


7. 将迭代算法和不动点定理关联在一起
将迭代算法和不动点定理做出以下关联

故只要证明 function F 是单调的
之前已经说明 transfer function 是单调的,故只要证明 join/meet function 是单调的

到这里为止,我们可以用格的数学概念和不动点定理严格证明:
数据流分析的迭代算法一定能停下来(到达不动点),并且一定是最大(最小)不动点
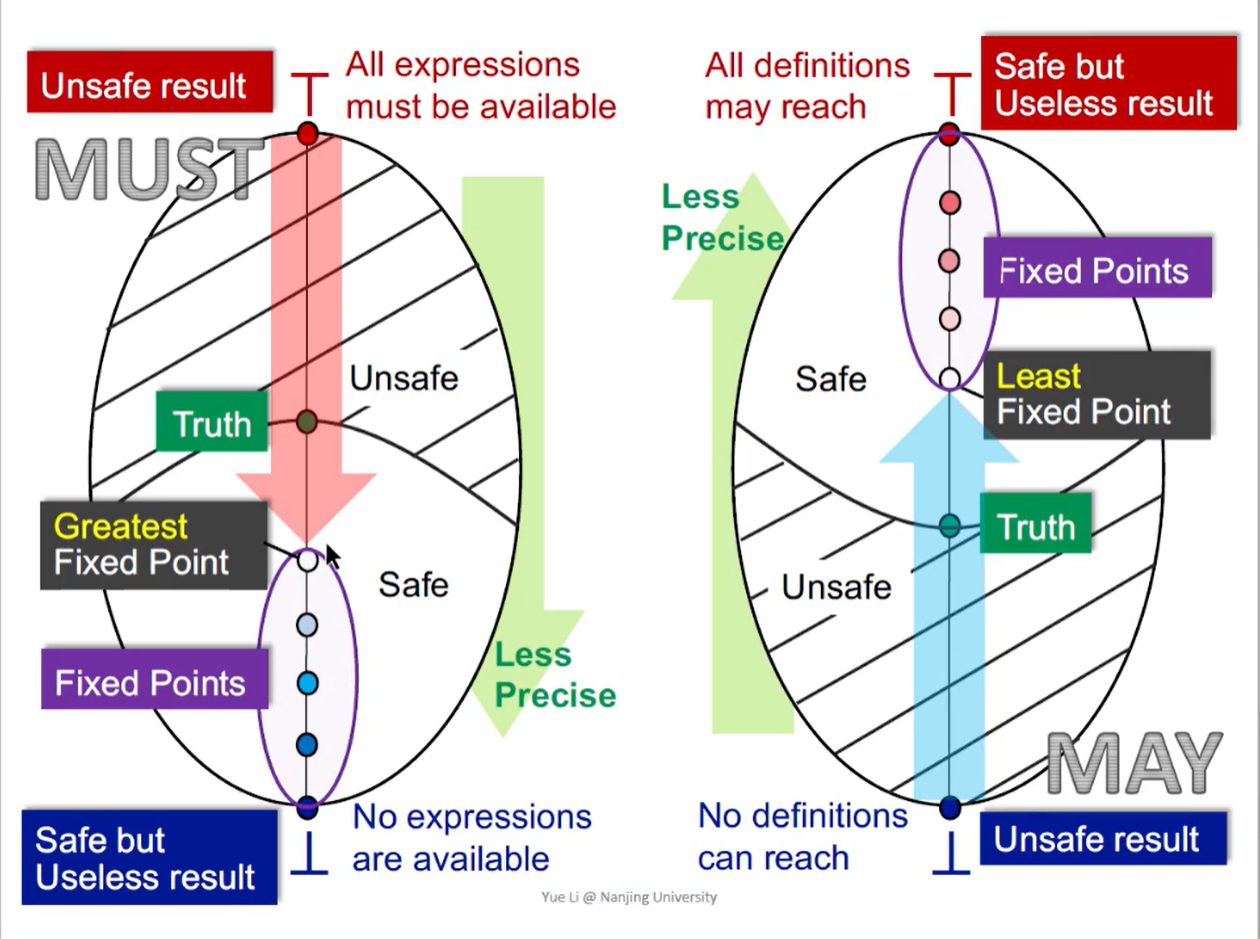
8. 格的视角下的 May / Must Analysis
无论是 May Analysis 还是 Must Analysis,都是从 unsafe 的情况向 safe but useless 的情况迭代
9. MOP
Meet-Over-All-Paths Solution(MOP)
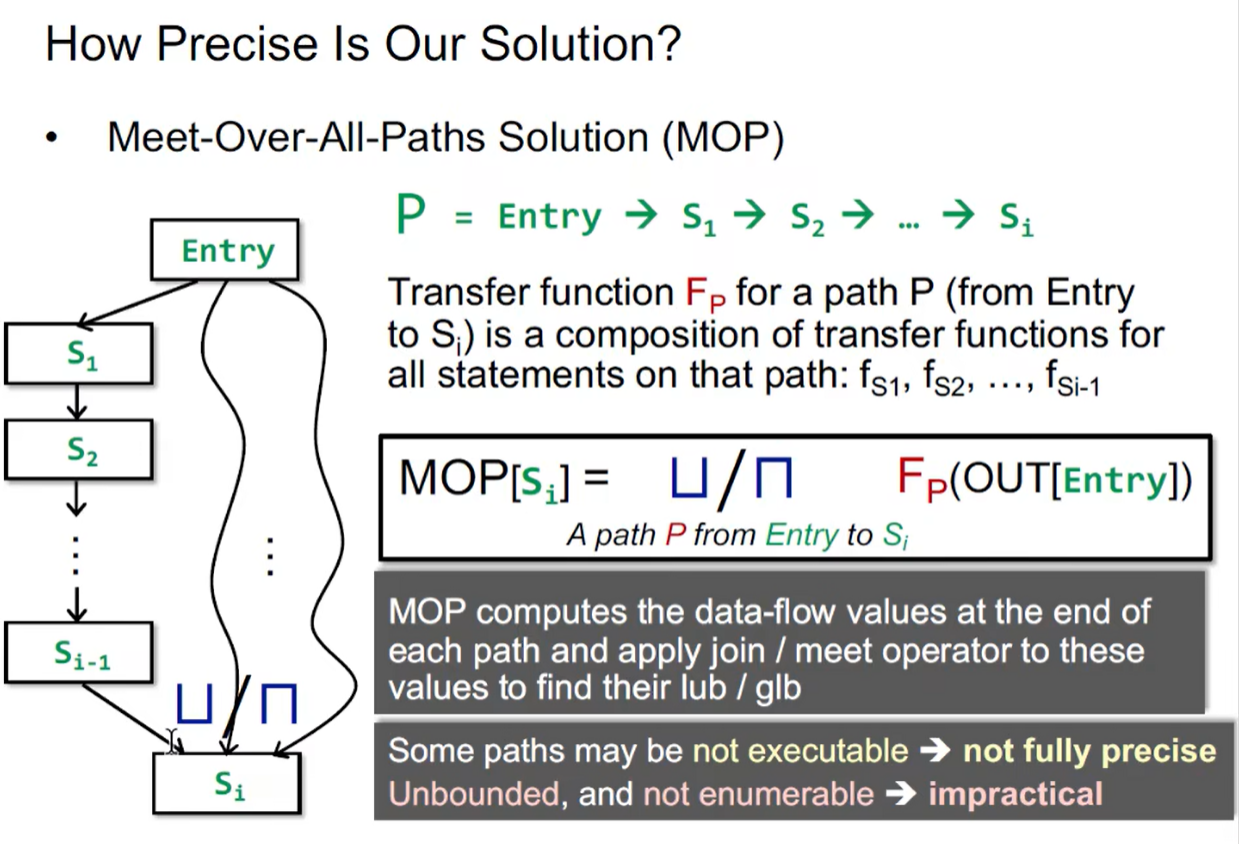
迭代算法与 MOP 的比较:
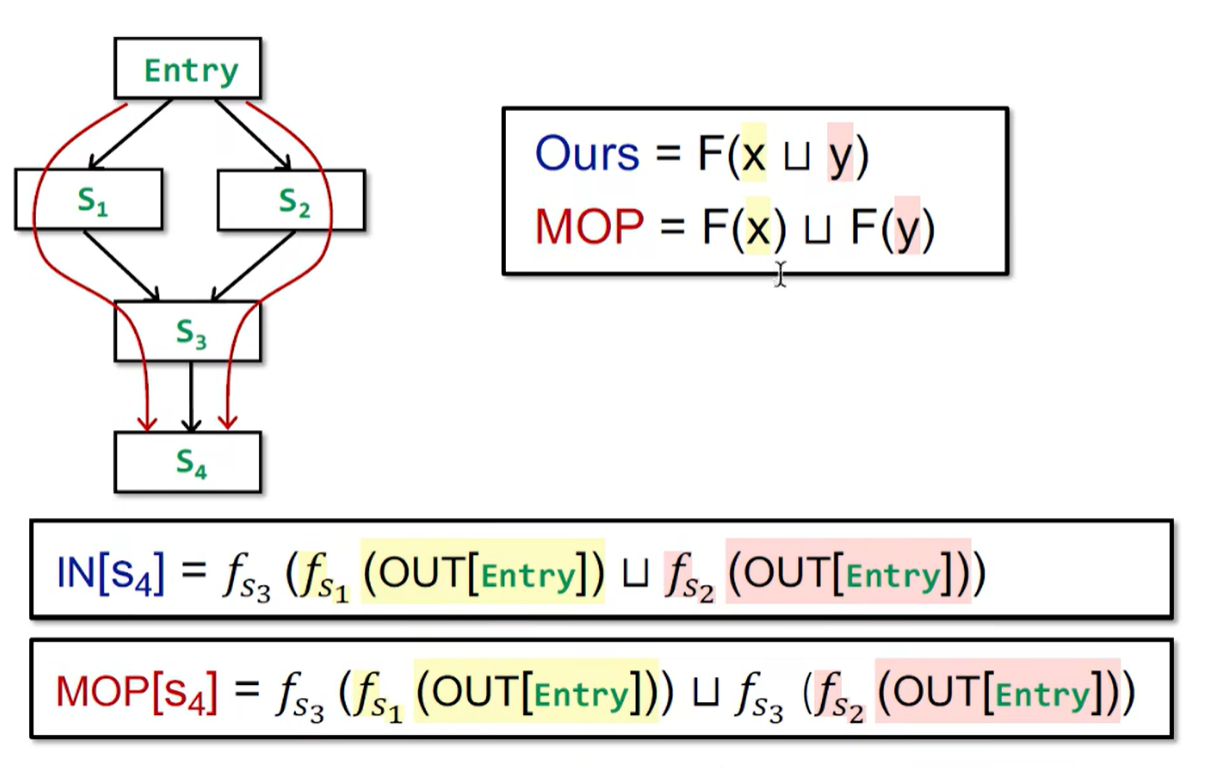

迭代算法得到的结果没有 MOP 准确,但当 Transfer Function 满足分配律的时候,迭代算法可以做到和 MOP 一样准确(可以用集合的交并进行操作的 Transfer Function 都是满足分配律的)
10. 常量传播分析(Constant Propagation Analysis)
常量传播(Constant Propagation):对于给定的变量 x,在某一个 program point p,确定该变量是否确保持有一个常量值(must analysis )
与之前的数据流分析不同,常量传播 CFG 中每个节点的 IN 和 OUT 都是键值对 (x, v) 的集合(x 表示变量名, v 表示变量持有的值)
根据数据流分析框架 (D, L, F) 来对常量传播分析进行定义:
- 常量传播分析的数据流是正向的(forward)
- 常量传播分析的格模型
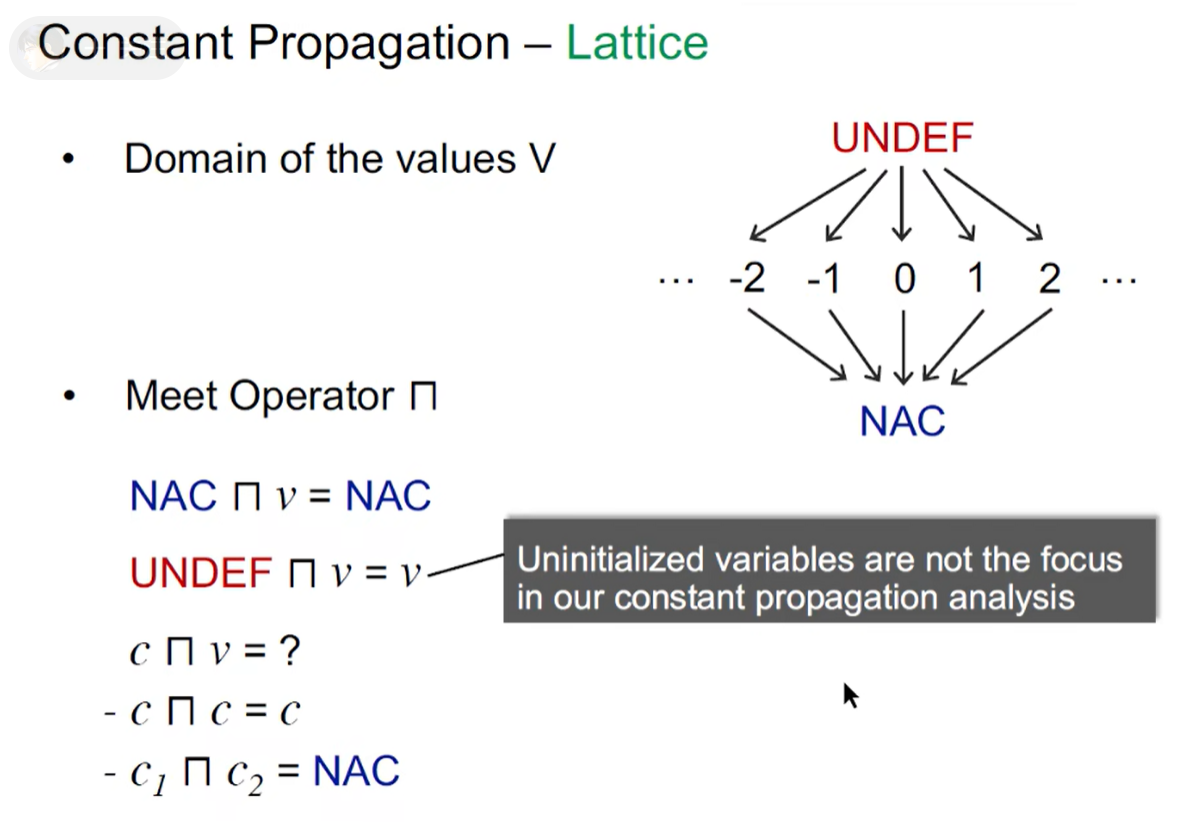
- 常量传播分析的转移函数

常量传播分析的 Transfer Function 不满足分配律
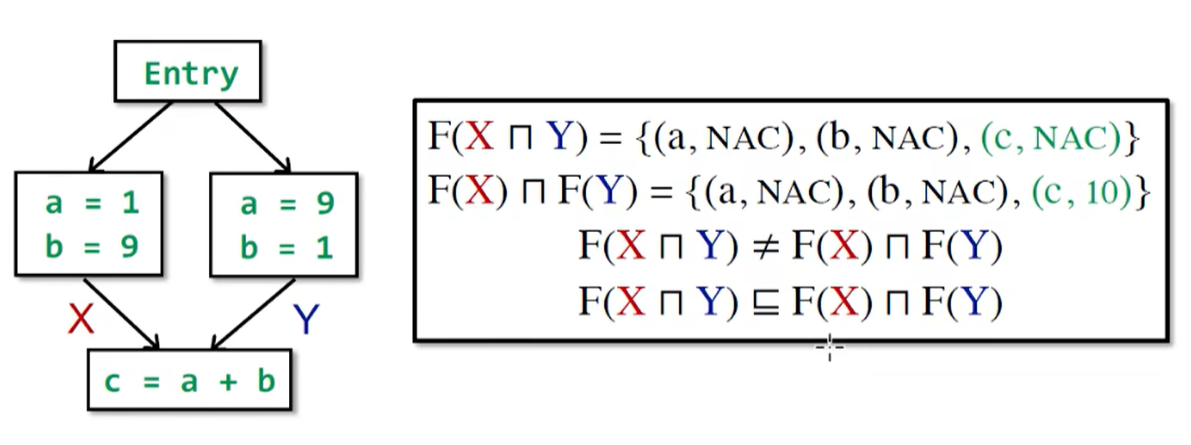
11. 工作列表算法
工作列表算法(Worklist Algorithm)是迭代算法的一种优化,在实际场景中更常用
迭代算法的主体操作流程清晰直观但有很多冗余步骤,工作列表算法可以做到每次仅对有变化的部分施加转移函数

本节重点
- 从函数的角度理解迭代算法
- 理解格的概念
- 理解不动点定理
- 用格来概括 may/must analysis
- 理解 MOP 和迭代算法之间的联系
- 常量传播分析
- 工作列表算法
05 - Interprocedural Analysis
1. 为什么需要过程间分析
仅对单个方法进行静态分析,若出现了对别的方法的调用,为了确保分析的正确性,只能认为该调用可以做任何事情,从而使得分析结果不够准确。例如,在常量传播分析中,分析 x = fun() 会认为 x 是 NAC,但方法 fun() 可能返回的是一个常数,即 int fun() { return 0; }
2. 调用图的构造
调用图:程序中调用关系的表示方式
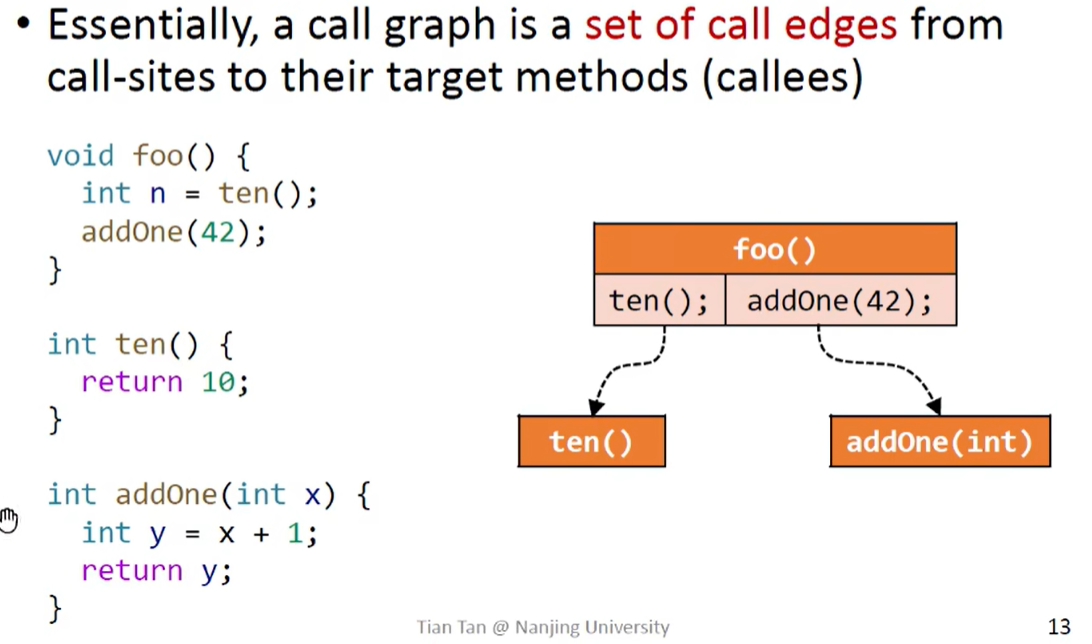
调用图的应用:过程间分析的基础,程序的优化、理解、debug、测试 ……
OO 语言的调用图的构造(以 JAVA 为代表):
- 类层次分析(CHA,Class Hierarchy Analysis):效率高
- 指针分析(k-CFA,Pointer Analysis):精确度高
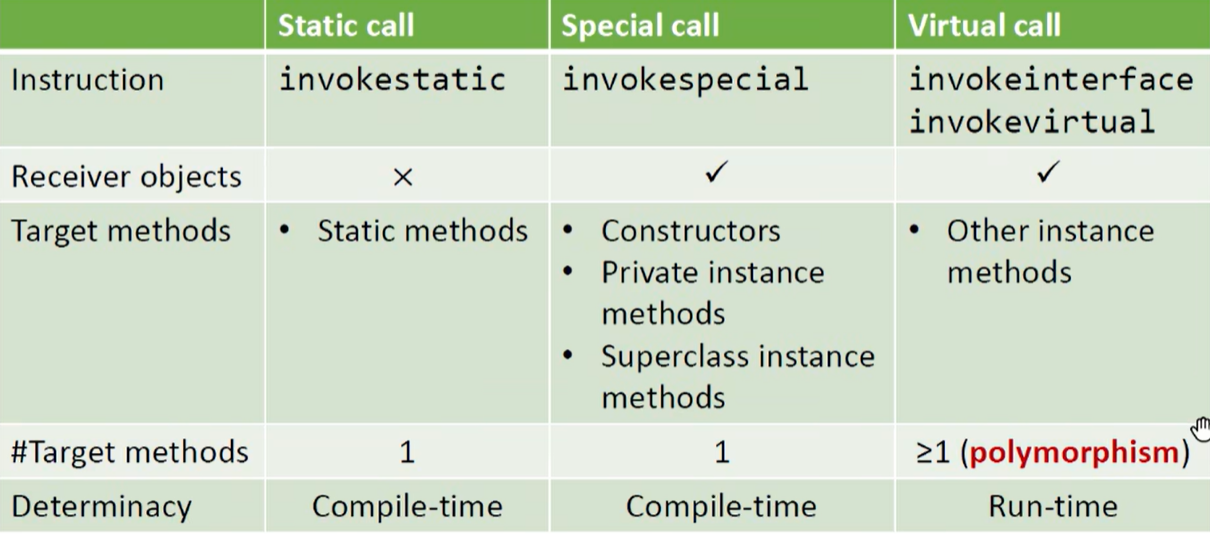
JAVA 中的方法调用共有五种,其中 invokedynamic 在此不做考虑,由于 Virtual Call 的目标方法是运行时动态确定的(多态),故构造调用图的难点和关键在于如何处理 Virtual Call
Virtual Call 的方法分派依据 receiver object 的类型 c 和方法的签名 m (形如 *<ClassType:ReturnType MehtodName(ParameterTypes)>*),定义函数 Dispatch(c, m) 去模拟运行时方法分派,总的思路是优先在子类中匹配,匹配不到则递归地到父类中匹配

类层次分析(Class Hierarchy Analysis)
适用于 IDE 等场景,快速分析并对准确性没有较高的要求
定义函数 Resolve(cs) 解析方法调用的可能的目标方法,分别处理 static call,special call 和 virtual call
注意 special call 中调用父类方法的时候需要递归寻找,为了形式统一使用用 Dispatch 函数
注意 virtual call 需要对对象的声明类型及其所有子类做 Dispatch(可能产生假的目标方法,不够准确)

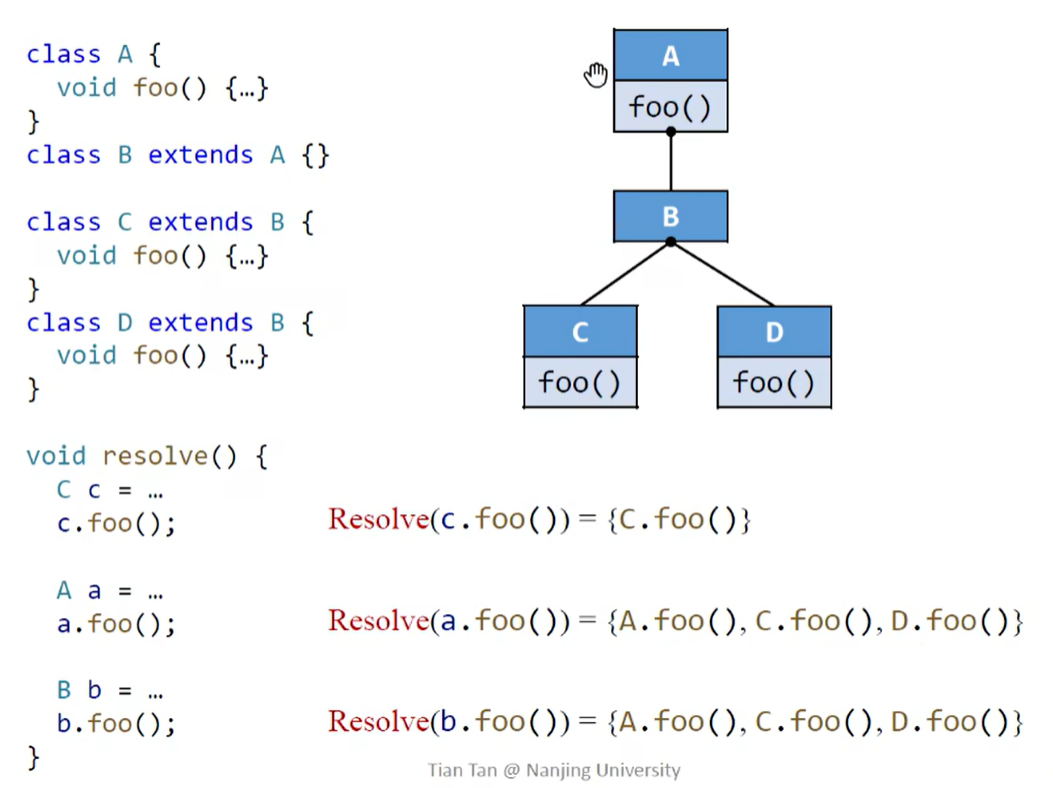
下面是 CHA 的一个例子,注意理解 Resolve( b.foo() )
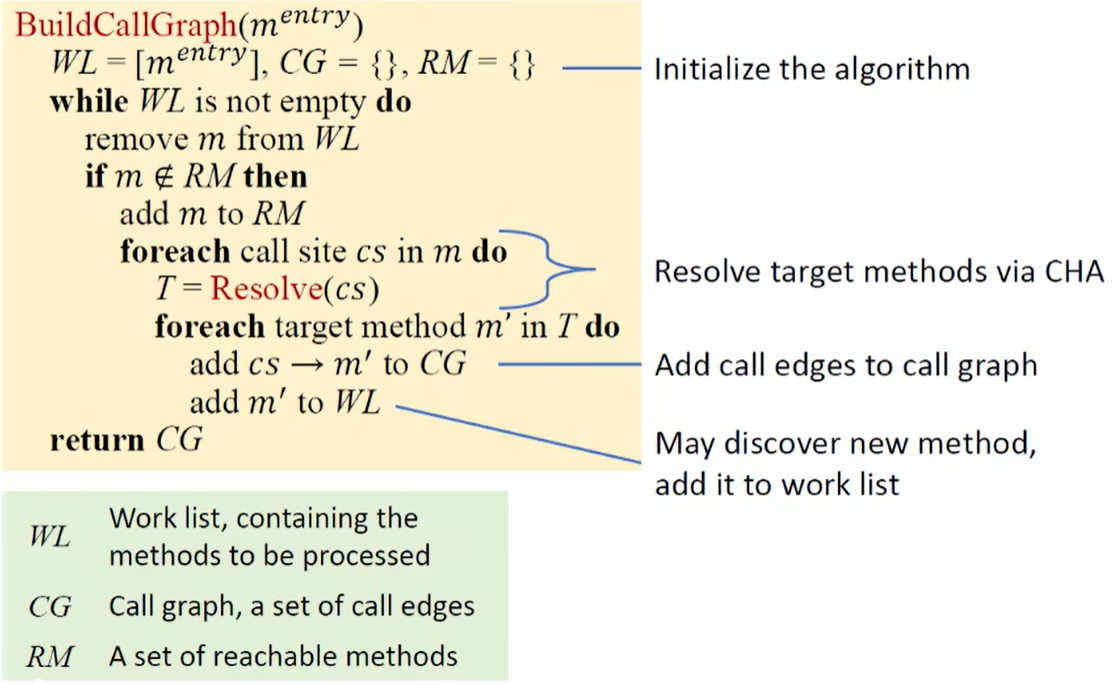
通过 CHA 来构造调用图:从入口方法(main)开始,对每一个可达的方法 m 中的每一个调用点 cs,解析目标方法(*Resolve(cs)*),重复该过程知道没有新的方法被发现。具体算法如下:
3. 过程间控制流图
回顾:控制流图(CFG)可以表示一个独立的方法的结构
过程间控制流图(ICFG,Interprocedural Control-Flow Graph)可以表示整个程序的结构,包含程序中每个方法自己的控制流图以及两类额外的边:从调用点指向被调用方法的 Call edges 和从被调用方法的返回语句指向返回点(即调用点的下一条语句)的 Return edges,额外的边的信息从构造的调用图中可以获取。概述如下图:

4. 过程间数据流分析
基于 ICFG 进行程序分析,其 Transfer Function 不仅需要正常的 Node Transfer 还要处理 Call Edge Transfer(用于传参) 和 Return Edge Transfer(用于传递返回值)
过程间常量传播分析(Interprocedural Constant Propagation)
在 ICFG 中保留了调用点到返回点之间相连的边(call-to-return edge),能使得 ICFG 能够传递本地数据流(单个 CFG 内产生的数据流)
在本地方法的 CFG 中的 Node Transfer 需要把调用点的左值变量 kill 掉(Return Edge Transfer 会覆盖这些变量的值)
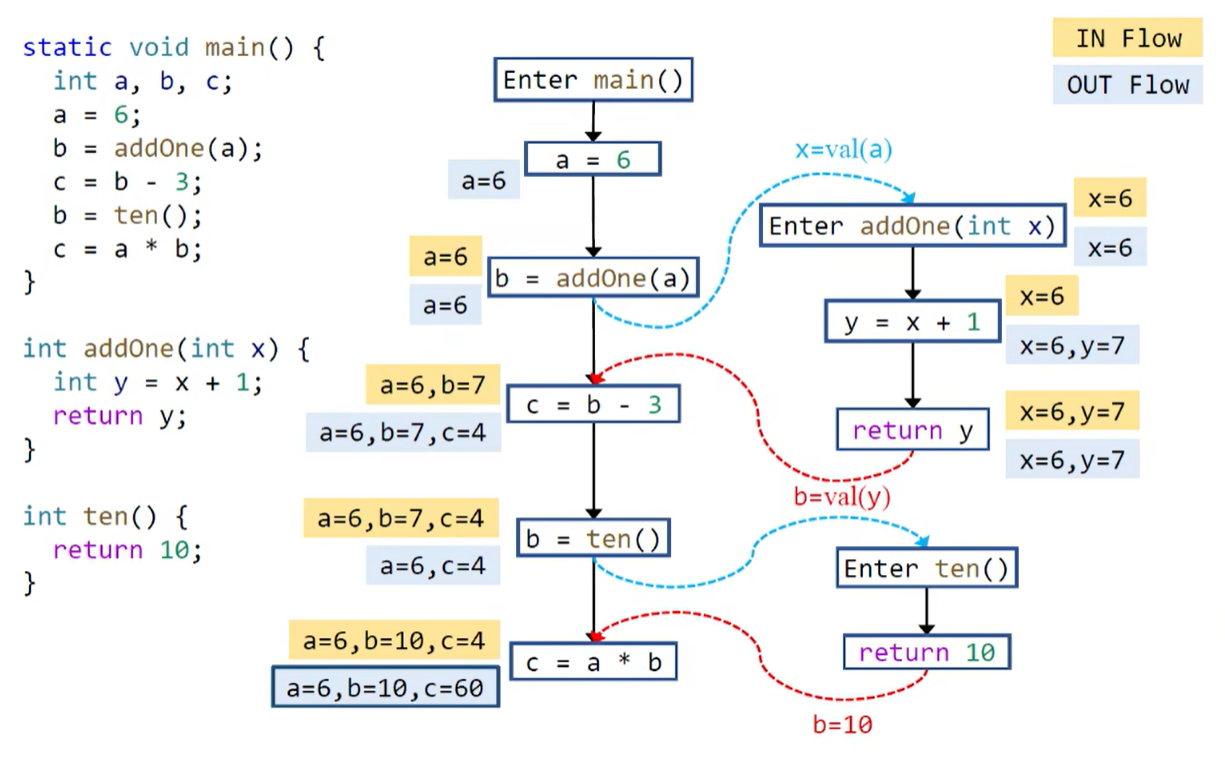
下面是一个详细示例:
本节重点
- 如何通过 CHA 构建调用图
- 过程间控制流图的概念
- 过程间数据流分析的概念
- 过程间常量传播分析
06 - Pointer Analysis
1. 为什么需要指针分析
基于指向关系进行分析,能有效避免 CHA 中出现 fake target 的问题
例如:针对语句 { A a = new A(); a.fun(); },CHA 在解析 a.fun() 时会得到所有 A 类型及其子类的签名为 fun() 的方法,而使用指针分析则可以找到唯一的一个目标方法,提高分析的准确性
2. 指针分析的介绍
指针分析是基础的静态分析,计算一个指针能够指向内存中的哪些地址
对于面向对象语言,以 JAVA 为例,指针分析计算一个指针(variable or field)能够指向哪些对象
指针分析可以看作一种 may analysis,计算结果是一个 over-approximation

概念辨析:指针分析 vs. 别名分析
指针分析回答的问题:Which objects a pointer can point to ?
别名分析回答的问题:Can two pointers point to the same object ?
别名分析的结果可由指针分析的结果推到而来
3. 影响指针分析的关键要素

堆抽象(Heap Abstraction)
为了保证静态分析能够终止,对堆内存进行建模,把 动态分配的无限的具体对象 构建成 有限的抽象的对象
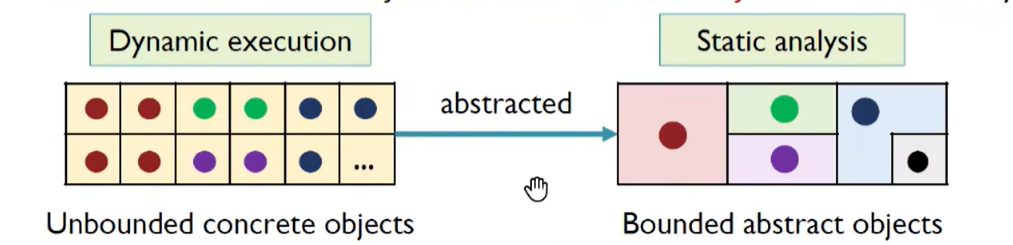
调用点抽象技术(Allocation-Site Abstraction)
将实例对象抽象成创建点,每个创建点建立一个抽象对象,用来表示该创建点分配的具体对象(在循环中的同一个创建点实际运行时会创建多个具体对象,但由于只有一个创建点只会创建一个抽象对象)
上下文敏感(Context Sensitivity)
上下文敏感的分析中,对同一个方法的不同调用进行区分,对每一个上下文都分析一次目标方法
上下文不敏感的分析中,对同一个方法的不同调用做数据流的合并处理,只分析一次,可能丢失精度
流敏感(Flow Sensitivity)
流敏感的分析是尊重语句的执行顺序的,程序中每个位置都维护了一个包含指向关系的 map
流不敏感的分析是忽视控制流的顺序的,整个程序只维护了一个包含指向关系的 map
分析域(Analysis Scope)
全程序分析:计算程序中所有指针的信息,服务所有可能的应用
需求驱动分析:只计算需要用到的指针的信息,服务特定的应用
4. 指针分析需要分析的语句
指针分析只关注 Pointer-Affecting Statements
JAVA 中的指针:
- 本地变量(local variable)e.g. x
- 静态字段(static field)e.g. C.f
- 实例字段(instance field)e.g. x.f
- 数组元素(array element)e.g. array[i]
在数组元素的指针分析中,忽略数组下标,把整个数组视作一个单独的 field
处理静态字段的方式与处理本地变量相似,处理数组元素的方式与处理实例字段相似
JAVA 中的 pointer-affecting statements:
- 创建 New x = new T()
- 赋值 Assign x = y
- 存储 Store x.f = y
- 加载 Load y = x.f
- 调用 Call r = x.k(a, …)
本节重点
- 什么是指针分析
- 理解影响指针分析的关键要素
- 理解指针分析需要分析哪些内容
07 - Pointer Analysis(Foundations)
本章节介绍使用调用点抽象技术、上下文不敏感、流不敏感的全程序指针分析
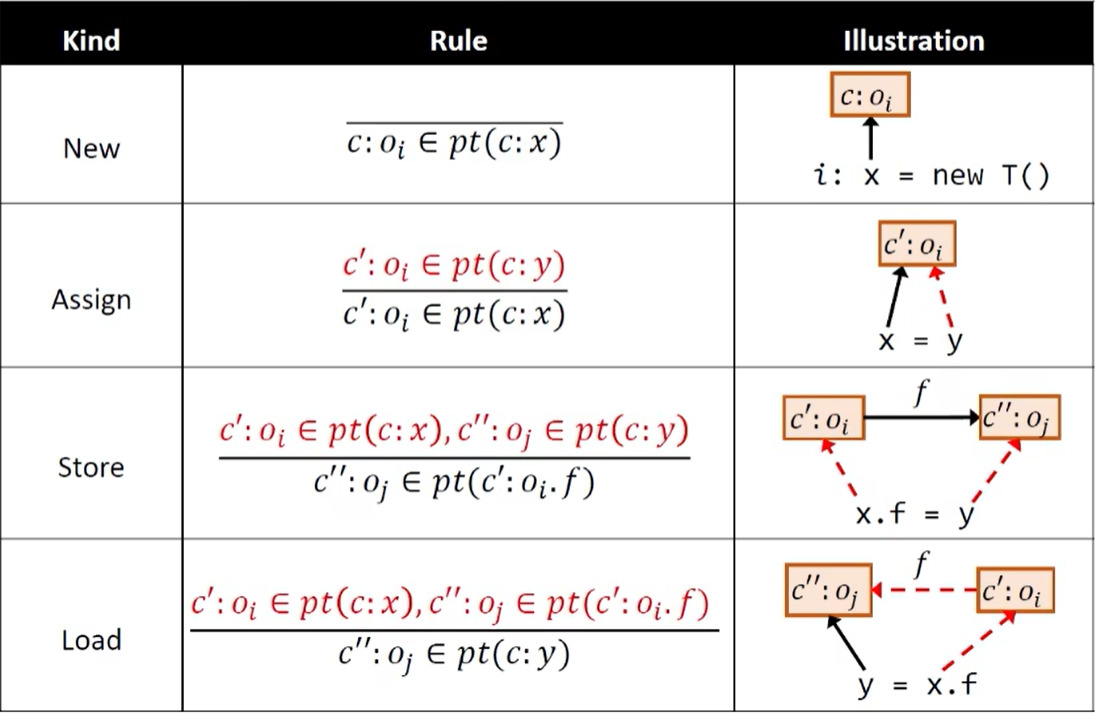
1. 指针分析的规则
在 JAVA 的指针分析中,常用流不敏感的方式(效率高,精度损失可接受)
指针分析的域及其表示:

不同语句的指针分析规则:
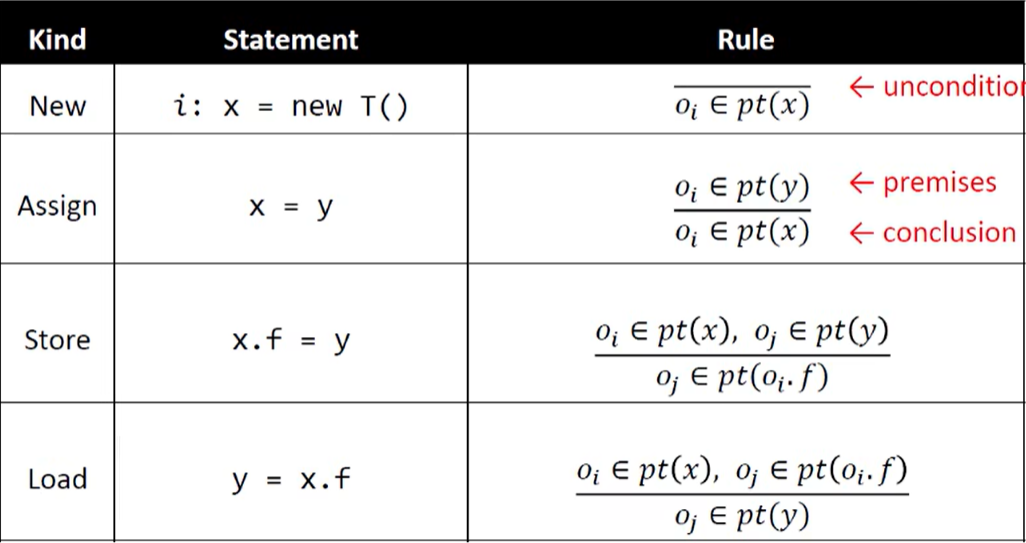
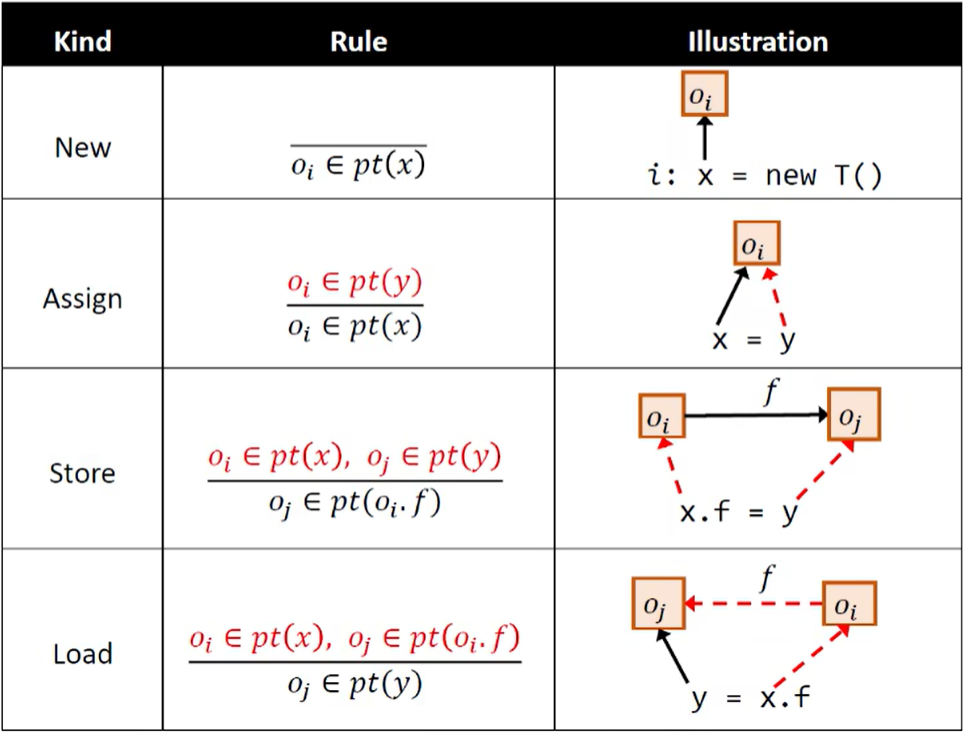
2. 指针分析的实现
指针分析要在指针间传播指向信息,指针分析解决的是指针间的包含约束系统的问题
实现指针分析的关键在于:当指针集 pt(x) 改变时,要把更新的信息传播给其他与 x 相关的指针
实现方式:用图去连接相关联的指针,当指针集 pt(x) 改变时,把更新的信息传播给 x 的后继
指针流图(Pointer Flow Graph,PFG)
指针流图的节点为 Pointer = *V ∪ (O × F)*,可能是变量或抽象对象的字段
指针流图的边为 Pointer × Pointer,由 x 指向 y 的边表示 x 指向的对象有可能被 y 指向
指针流图的边由程序中的语句和处理指针分析的规则来确定:
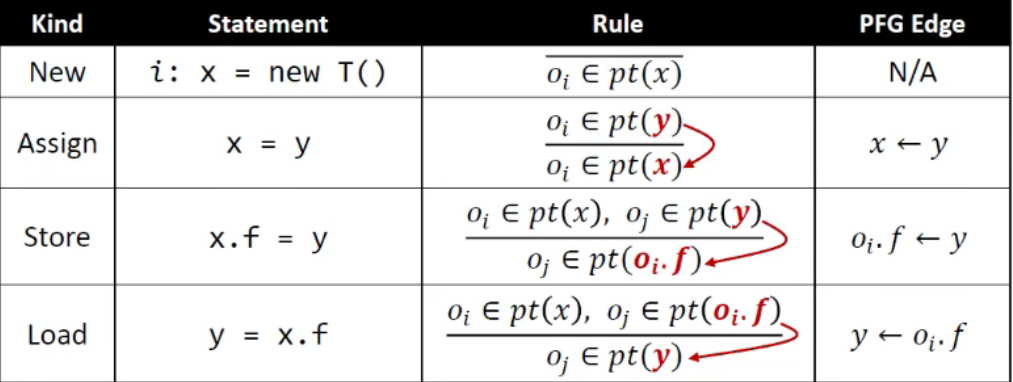
通过指针流图,指针分析问题可以转化为在指针流图上求解传递闭包的问题
指针分析的复杂性在于构建指针流图和传播指向信息相互依赖(在指针分析的过程中,指针流图也在不断更新迭代,从而再次影响指针分析的过程):

3. 指针分析的算法
完整的算法过程:

关于算法中 WL,即 Worklist 的解释:

4. 带有方法调用的指针分析
过程间的指针分析需要构建调用图,使用 CHA 基于声明类型解析目标方法可能产生 fake target,在指针分析中,可以基于变量的指针集进行解析,得到更准确的调用图(on-the fly call graph construnction)
方法调用的指针分析规则:
一个方法调用要做的四件事:Dispatch;传 receiver object;传参数;传返回值

思考:为什么不在 PFG 中添加由 x 到 m_this 的边?

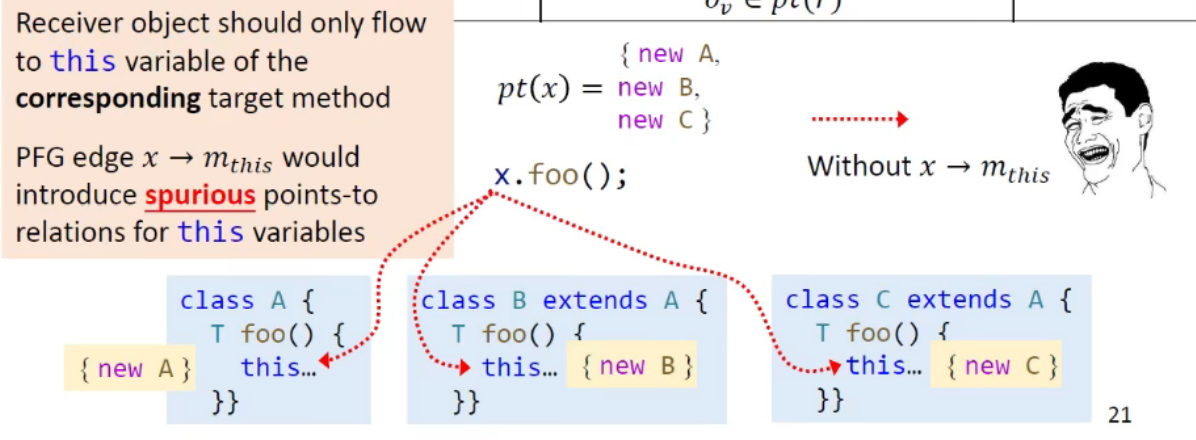
过程间指针分析和调用图的构建相互依赖,同时进行

带有方法调用的指针分析的算法实现:
(黄底内容为新增部分)

本节重点
- 理解指针分析的规则
- 理解指针流图
- 理解指针分析的方法
- 理解指针分析处理方法调用的规则
- 理解过程间指针分析算法
- 理解即时调用图构建
08 - Pointer Analysis(Context Sensitivity)
本章节介绍使用调用点抽象技术、上下文敏感、流不敏感的全程序指针分析
1. 上下文敏感指针分析介绍
为什么需要上下文敏感技术:
在动态执行的时候,一个方法可能被调用多次,而不同调用的上下文不同(传参不同、返回点不同),故在上下文不敏感的指针分析中,不同调用上下文混合的数据流在程序中传播,产生假的数据流,影响程序分析的精度;引入上下文敏感技术,区分不同上下文之间的数据流,可以提升程序分析的精度
上下文的表示方式:
使用调用点来作为上下文:用一系列调用点来链式表示每个上下文(栈抽象)
上下文敏感的实现:

上下文敏感的堆抽象:
在 OO 程序中,经常需要修改堆上对象,因此在实际情况中,上下文敏感技术需要应用于堆抽象
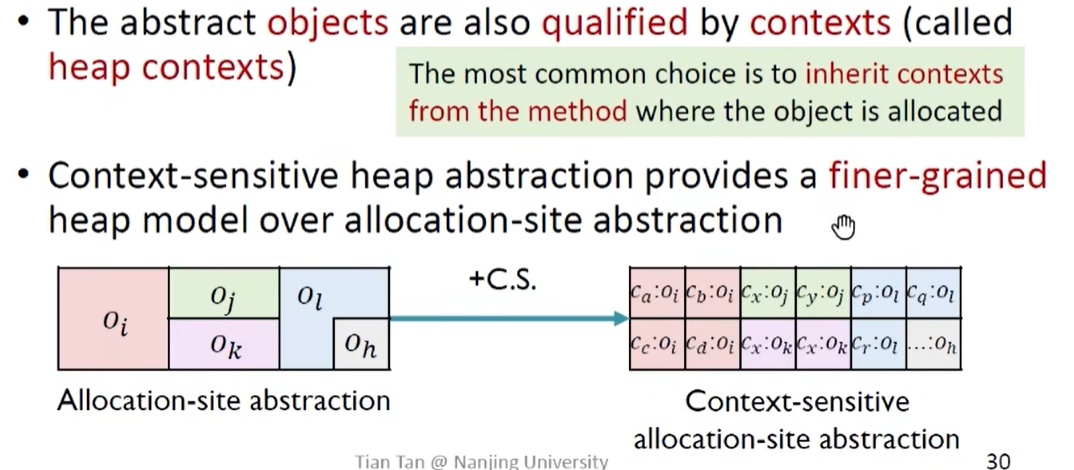
为什么上下文敏感的堆抽象能够提升分析精度:


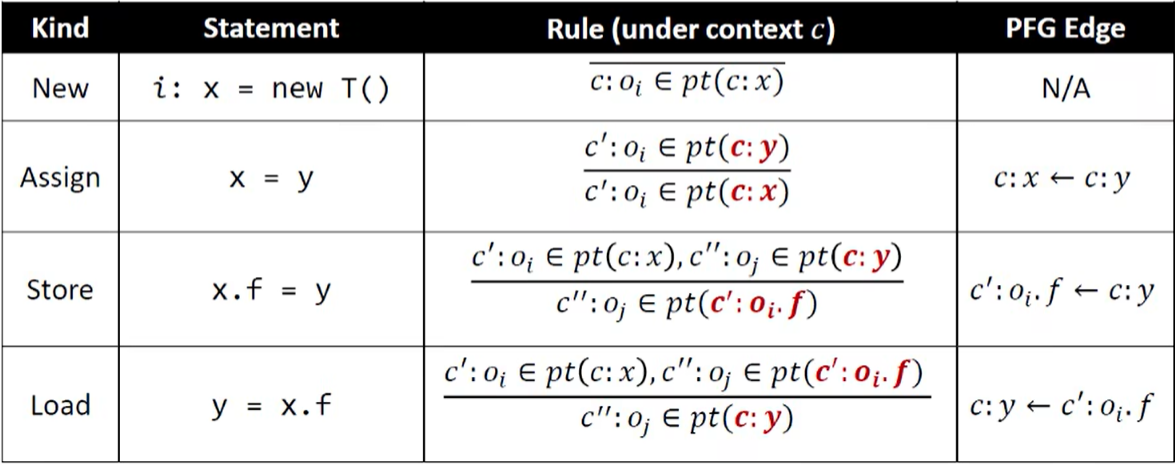
2. 上下文敏感指针分析规则
上下文敏感指针分析的域及其表示:

上下文敏感指针分析的规则:

3. 上下文敏感指针分析算法
基本思路和上下文不敏感的指针分析相似,即:

其中 PFG with C.S. 是一个有向图,定义如下:

PFG with C.S. 边的建立:

上下文敏感指针分析完整算法:

4. 上下文敏感技术的变种
上下文敏感指针分析算法中 Select 方法的具体实现方式
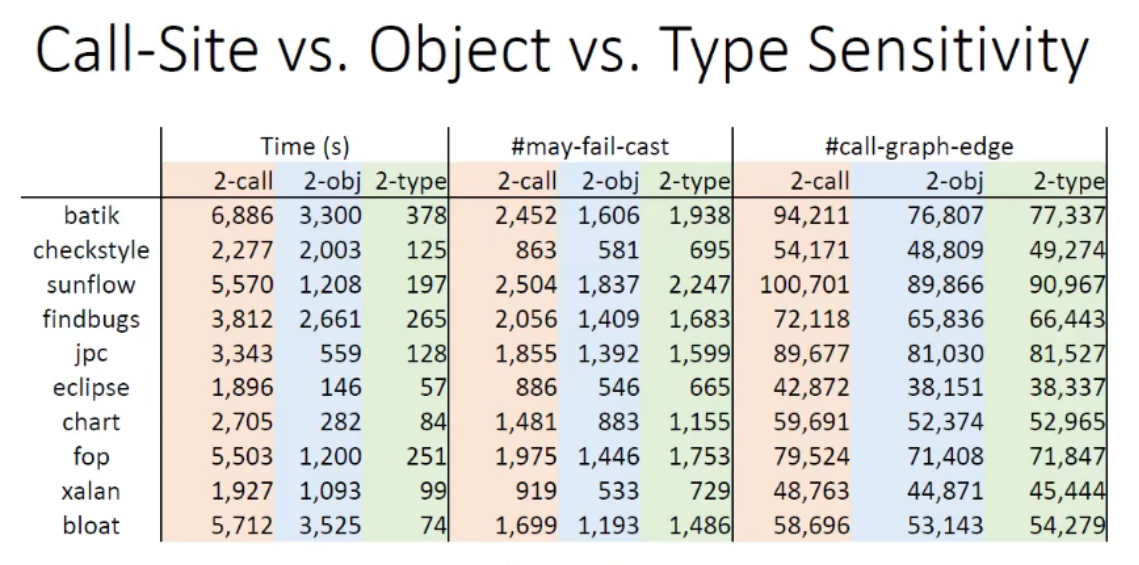
调用点敏感(Call-site Sensitivity)

为了避免产生过多的上下文,保证指针分析在合理的时间内完成,需要对调用链的长度进行限制(e.g. 递归调用能够产生很长的调用链),故引入 k-Limiting Context Abstraction,即选用最后的 k 个调用点作为上下文:

调用对象敏感(Object Sensitivity)

在 OO 语言的实际应用中,调用对象敏感效果比调用点敏感速度更快、效果更好
调用类型敏感(Type Sensitivity)

调用类型敏感是对调用对象敏感的一种粗粒度的抽象,获取了更快的分析速度,牺牲了精度
三种上下文敏感技术变体的对比
本节重点
- 上下文敏感的概念
- 上下文敏感的堆抽象的概念
- 为什么上下文敏感和上下文敏感的堆抽象能够提升分析的精度
- 上下文敏感的指针分析的规则
- 上下文敏感指针分析的算法
- 常见的上下文敏感技术的变体
- 常见的上下文敏感技术的变体的不同与联系
09 - Static Analysis For Security
1. 信息流安全
与访问控制不同,信息流表示一种端到端的数据流动
给程序中的变量赋予不同的密级(Security Level)以构建实现信息流安全的策略
密级可以用格(Lattice)进行建模,虽然二元密级(Low & High)最为常见和常用,但是也可以存在复杂的密级结构:
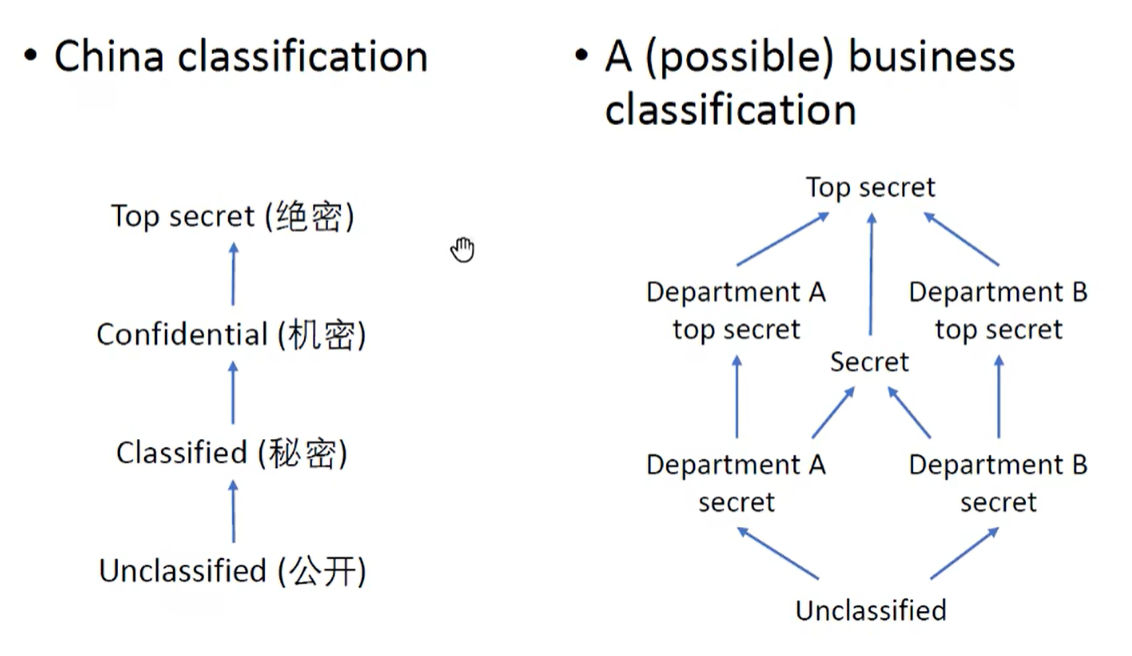
非干涉策略(Noninterference Policy):不允许信息从高密级流向低密级
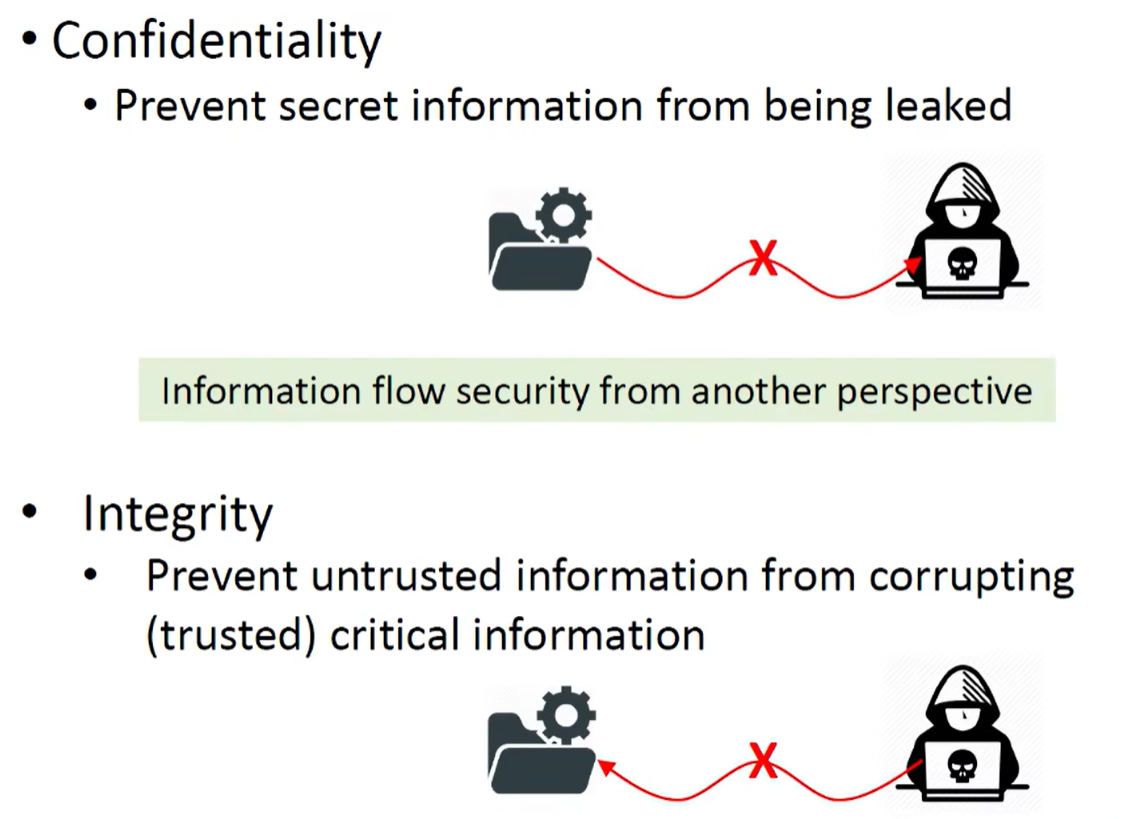
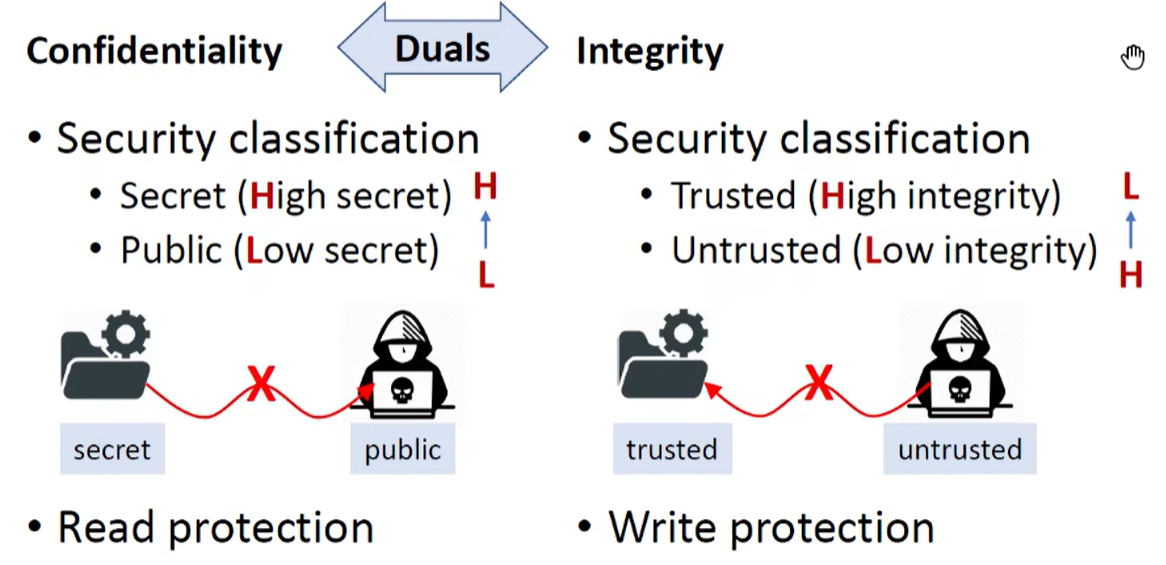
2. 保密性和完整性
3. 显式流和隐藏信道
显式流(explicit flow):通过直接拷贝进行的信息流动
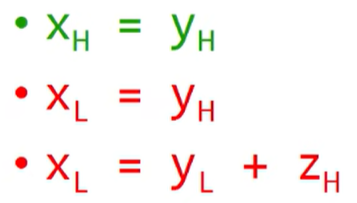
隐式流(implicit flow):控制流受到高密级信息的影响,如果产生的副作用能被观测到则会信息泄露

隐藏信道(hidden channel):不是用来传递信息流的内容将信息间接地传递出去,造成信息泄露

就保密性而言,隐藏信道泄露的信息量有限,就完整性而言,隐藏信道不会造成什么危害,故应当优先处理显式流中的信息流安全问题
4. 污点分析
污点分析(Taint Analysis)将程序中的数据分为两类:
- Data of interest,将某些标签与其进行绑定,称之为污点数据(tainted data)
- Other data,称之为非污点数据(untainted data)
污点数据的源头称为 source,实际情况中,污点数据通常来源于某些方法(sources)的返回值
污点分析追踪污点数据,观测其是否会流入某个特定的地方(sink) ,实际情况下通常是某些方法传参
污点分析的两种应用:

污点分析和指针分析本质上具有高度一致性,可以依据指针分析来做污点分析:





本节重点
- 信息流安全的概念
- 保密性和完整性的概念
- 显式流和隐藏信道的概念
- 如何使用污点分析的检测有安全隐患的信息流
实验作业部分
A1
- 为 Java 实现一个活跃变量分析(Live Variable Analysis)
- 实现一个通用的迭代求解器(Iterative Solver),用于求解数据流分析问题,也就是本次作业中的活跃变量分析
LiveVariableAnalysis 类提供了一个活跃变量分析器,提供算法执行过程中所需要的接口(图中红色的方法标注),作为 Solver 类的一个私有变量
Solver 类执行整个算法流程(大致分为初始化和循环体两个模块),分析结果以一个 DataflowResult 类的对象返回
注意 LiveVariableAnalysis 类只关注逻辑,IN, OUT, EXIT, ENTRY 等信息由 DataflowResult 类通过 inFacts 和 outFacts 两个 Map 管理
注意作业中为了简化实现难度没有使用 basic blocks,以单条语句为单位处理

A2
- 为 Java 实现常量传播算法
- 实现一个通用的 worklist 求解器,并用它来解决一些数据流分析问题,例如本次的常量传播
与 A1 的任务总体结构相同,理解常量传播和 worklist 的实现方式并读懂提供的框架源码即可
注意 newBoundryFact() 需要将方法的参数初始化为 NAC(参数不由方法本身决定,故必不是常量)
注意 transferNode() 的返回值为一个布尔类型,worklist 算法中不需要重复判断 OUT 是否被改变
注意 CPFact 类的设计,变量不在某个 CPFact 对象中视为 UNDEF
(有部分隐藏用例没有通过,大概猜测是在 evaluate() 方法中一些除了 Var, IntLiteral 和 BinaryExp 其他一些特殊类型的 expression 没有考虑的缘故,暂且搁置)
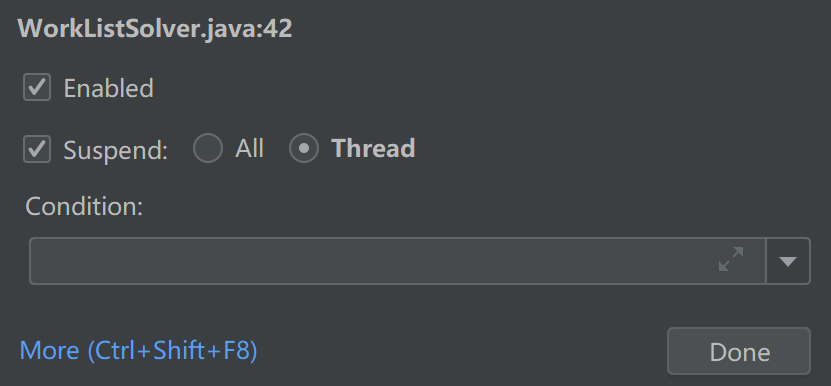
关于 debug:在 IntelliJ IDEA 中进行断点调试的时候,出现 ”Skipped breakpoint at … because it happened inside debugger evaluation“,打条件断点的地方被跳过,是由于测试时使用了多线程,将断点设置中 Suspend 选项的 All 改成 Thread 即可(如图所示)
A3
- 为 Java 实现一个死代码(dead code)检测算法
该死代码检测作业需要找出两种死代码:不可达代码和无用赋值
不可达代码又分为控制流不可达(e.g. Return 语句之后的代码)和分支不可达(e.g. 条件跳转处的条件为常量)
本次作业需要用到 A1 中实现的活跃变量分析(寻找无用赋值)和 A2 中实现的常量传播分析(寻找分支不可达的代码),并新补充实现 DeadCodeDetection 类中的 analyse 方法
在 analyse 方法中,已经构建了程序的控制流图、常量传播分析结果和活跃变量分析结果,需要以此为据找出可以被判定为死代码的语句,以一个集合的形式返回
一开始的思路是直接寻找死代码语句,但发现由于在数据流不向后继续传递,在确定一条语句为死代码后难以判断其后继语句是否为死代码,故转换思路,通过确定活代码来反推死代码,总体思路为从程序入口处开始,借助常量传播分析结果和活跃变量分析结果,在控制流图上遍历所有可能被执行的活代码并标记,没有被标记到的节点即为死代码
A4
- 为 Java 实现一个类层次结构分析(Class Hierarchy Analysis,CHA)
- 实现过程间常量传播
- 实现过程间数据流传播的 worklist 求解器
类层次结构分析部分需要实现 buildCallGraph、resolve 和 dispatch 三个方法,课件中已经给出了相应的算法流程,模拟实现即可
- callSite.getMethodRef().getDeclaringClass() 获取调用点的对象的声明类型
- callSite.getMethodRef().getSubsignature() 获取调用点方法的子签名(一个方法的子签名只包含它的方法名和方法签名的描述符)
- 成员变量 hierarchy 中包含了所有类和接口的继承和实现关系
过程间的常量传播需要考虑 transferNode 和 transferEdge 两种情况:
- transferNode 分为 transferCallNode 和 transfeNonCallNode:由于调用由 transferEdge 处理,transferCallNode 只需要做恒等传播;而 transfeNonCallNode 与 A2 中的非过程间常量传播的 transferNode 相同
- transferEdge 分为 transferCallToReturnEdge、transferCallEdge 和 transferReturnEdge:transferCallToReturnEdge 需要将调用点的左值 kill 掉(如果存在的话);transferCallEdge 需要完成参数的值的传递;transferReturnEdge 需要完成返回值向调用点左值的赋值(如果存在的话)
(注意 transferEdge 的返回值是一个新的 Fact,不改变已有的 Fact)
e.g. 下图中蓝色虚线箭头为 callEdge,红色虚线箭头为 returnEdge,黑色虚线箭头为 callToReturnEdge
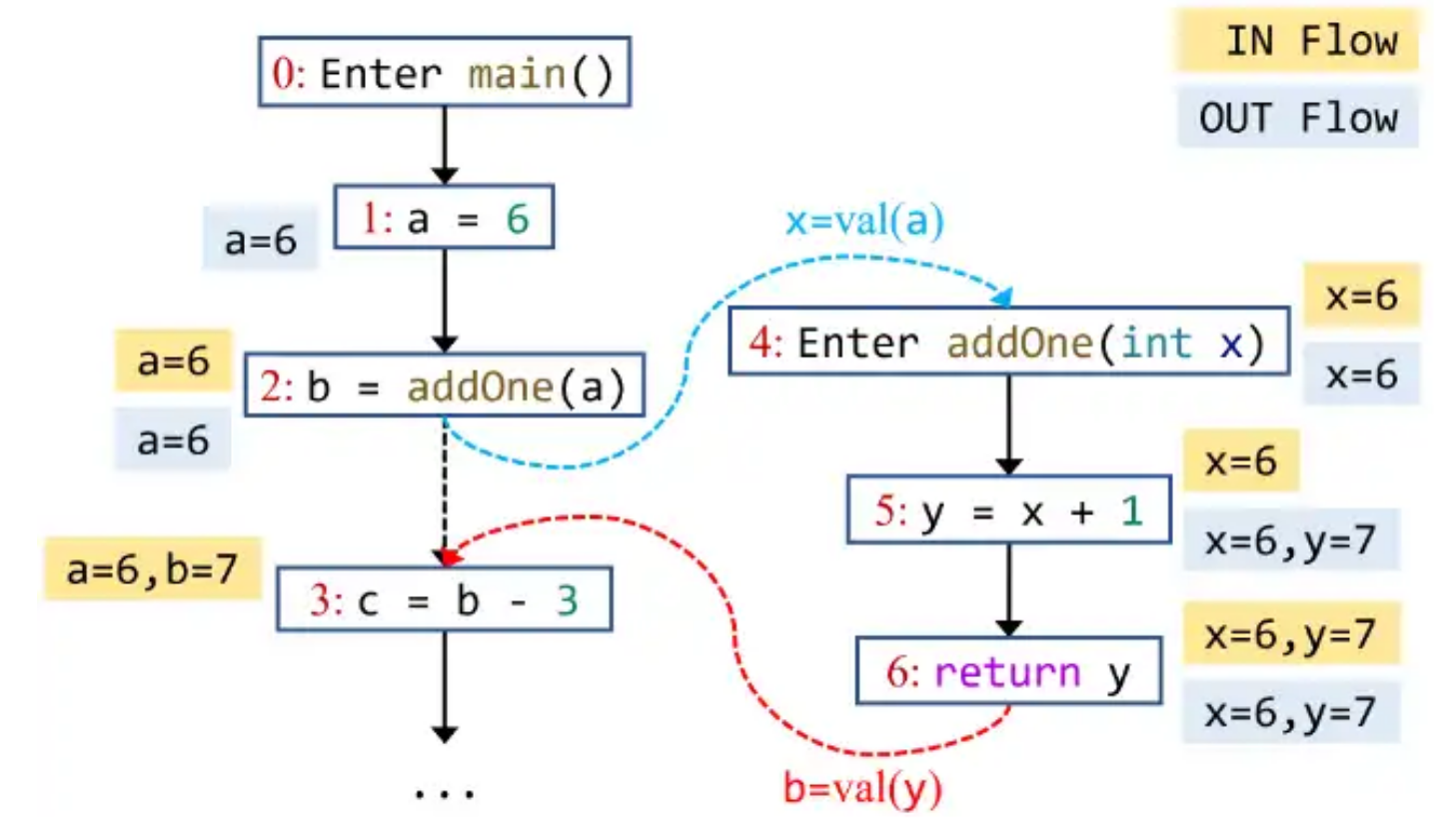
在实现 worklist 求解器时,注意与之前实现的不同之处有:
初始化时,需要对所有的 entry method 的 entry 节点进行 newBoundaryFact(可使用 icfg.entryMethods().toList() 获取所有的 entry method)
执行算法流程时,每个节点的 inFact 不再是和所有前驱节点的 outFact 做 meet 操作获得,而是和所有汇入的边所带来的 Fact 做 meet 操作获得
A5
- 为 Java 实现非上下文敏感的指针分析
- 为指针分析实现一个调用图的实时构建算法
作业文档足够详细,难度不大,按照算法流程实现即可,注意:
- 每个方法可能有多个返回值,也有可能没有返回值
- 处理方法调用时需要的 dispatch 方法已经给出(*resolveCallee()*)可直接调用
- 新引入的静态字段、静态方法调用和数组在需要算法中进行处理的位置
- var.getStoreFields()、var.getLoadArrays()、var.getInvokes() 等接口可直接获取变量相关的语句
- AddReachable 方法使用了访问者设计模式
- 提供的框架将算法中 Δ 的计算融入了 propagate 方法中
参考算法流程:
1 | Solve(m_entry): |
A6
- 为 Java 实现一个上下文敏感的指针分析框架
- 作为指针分析的一部分,随着指针分析一起实现调用图(call graph)构建
- 实现几种常见的上下文敏感策略(context sensitivity variants)
与 A5 相似,注意上下文的正确对应即可
A7
开放性作业
- 为 Java 实现一个 alias-aware 的过程间常量传播分析
在 A4 的基础上,利用 A6 中实现的指针分析的分析结果,得到更精确的过程间常量传播分析
A4 在 A3 的基础上,解决了把所有方法调用的返回值全部置为 NAC 的问题
A7 在 A4 的基础上,解决了把所有 load 语句(e.g. x = y.f)给变量的赋值全部置为 NAC 的问题
简言之就是,对于 load 语句 x = y.f,找出所有形如 z.f = w(z.f 满足条件是 y.f 的别名)的 store 语句,将所有变量 w 对应的值做 meet 操作并赋值给 x
满足互为别名的条件:
- 实例字段(x.f 和 y.g)
- 字段 f 和字段 g 相同
- 变量 x 和变量 y 对应的指针集有交集
- 静态字段(T.f 和 Q.g)
- 字段 f 和字段 g 相同
- 类 T 和类 Q 相同
- 数组元素(a[i] 和 *b[j]*)
- 变量 a 和变量 b 对应的指针集有交集
- 变量 i 和变量 j 都不是 UNDEF 并且变量 i 和变量 j 都是常量时其值相等

修改 transferNonCallNode 方法,对所有 load 语句和 store 语句进行单独处理:
- 对于 load 语句,不做 A4 中的常量传播,找出将所有满足别名关系的 store 语句加以处理
- 对于 store 语句,需要将所有满足别名关系的 load 语句加入到 solver 的 worklist 中(本质上来讲,满足别名关系的 load 语句会动态地成为对应 store 语句的后继)
A8
开放性作业
- 为 Java 实现污点分析
污点分析和指针分析的不同之处在于,污点可以在对象之间传播(因为污点和数据内容相关),所以不仅需要在方法调用处处理 sources 和 sinks(获取污点数据/得到污点流),还需要额外进行污点传播
在方法调用中特殊的污点传播:由 base 变量传给 result;由参数传给 base 变量;由参数传给 result,这些规则会在初始化的时候作为输入给出,可以通过 TaintConfig 类的 getTransfer 方法调用
总的来说,污点分析需要与 A6 中实现的指针分析相结合,并实现以下规则:


我的思路:
TaintAnalysiss 中添加(实现)的主要 API:
- captureTaintObj:执行 Call(source) 规则,返回一个新的污点对象
- captureTaintTransfer:执行特殊的污点传播规则,方法内部调用链三个私有方法 captureBaseToResult、captureArgToBase 和 captureArgToResult,分别执行规则 Call(base-to-result)、Call(arg-to-base) 和 Call(arg-to-result)
- collectTaintFlows:执行 Call(sink) 规则,返回一个污点流的集合,即污点分析的结果
在分析有返回值的方法调用时,调用 taintAnalysis.captureTaintObj 获取污点对象,并将其加入 result 变量的指针集中
在分析方法调用时,调用 taintAnalysis.captureTaintTransfer 处理污点传播
出现的问题及解决方式:
当污点对象传播到某个变量的指针集中时,以该变量作为参数的方法调用可能已经被分析过,并且可能不会被再一次加入 worklist,导致分析结果有所遗漏(方法调用中特殊的污点传播的分析是安插在指针分析过程中的)
对 propagate 方法进行改进,若一个变量的指针集中有新流入污点对象,则从现有的调用图中获取所有的调用点,找到以该变量作为参数的调用点,并对该调用点单独执行一次 captureTaintTransfer