2022.09
9.5
标签:二叉树序列化,哈希表,DFS
思路:用序列化的方式表示子树,通过字符串比较来判断子树是否重复
具体操作:通过 dfs 将二叉树序列化成 “root(左子树)(右子树)” 的形式,中间过程包含了所有子树的序列化结果,通过哈希表来保存重复的子树的根节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
Map<String, TreeNode> serialToTree = new HashMap<>();
Set<TreeNode> repeated = new HashSet<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
dfs(root);
return new ArrayList(repeated);
}
private String dfs(TreeNode node) {
if (node == null) { return ""; }
String serial =
node.val + "(" + dfs(node.left) + ")(" + dfs(node.right) + ")";
if (serialToTree.containsKey(serial)) {
repeated.add(serialToTree.get(serial));
}
else { serialToTree.put(serial, node); }
return serial;
}
}
|
9.6

(暴力求解会超时)
标签:动态规划,哈希表
思路:分别计算每个字符的贡献,对于下标为 i 的字符,其在字符串中上一次出现在下标 j 处,下一次出现在下标 k 处,那么其贡献的个数为 (i-j) * (k-i)
具体操作:先扫描一遍字符串,把每个出现的字符及其对应的位置(下标)通过 list 保存下来并维护一个映射关系(为了计算方便需要,每个 list 开头为 -1,结尾为 s.length()),然后遍历扫描结果按照思路中的计算方法进行计算并累加求和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int uniqueLetterString(String s) {
Map<Character, List<Integer>> map = new HashMap<>();
for (int i = 0; i < s.length(); ++i) {
char ch = s.charAt(i);
if (!map.containsKey(ch)) {
map.put(ch, new ArrayList<>());
map.get(ch).add(-1);
}
map.get(ch).add(i);
}
int res = 0;
for (char ch : map.keySet()) {
List<Integer> tmp = map.get(ch);
tmp.add(s.length());
for (int i = 1; i < tmp.size() - 1; ++i) {
res += (tmp.get(i) - tmp.get(i-1)) * (tmp.get(i+1) - tmp.get(i));
}
}
return res;
}
|
9.7
思路:通过 split(“\s+”) 方法获取所有的单词(注意去掉前置和后置的空格,否则得到的单词中有空串)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public String reorderSpaces(String text) {
int len = text.length();
String[] words = text.trim().split("\s+");
int numOfSpace = len;
for (int i = 0; i < words.length; ++i) {
numOfSpace -= words[i].length();
}
int intervalSpaceCnt = 0;
if (list.size() > 1) {
intervalSpaceCnt = numOfSpace / (list.size() - 1);
}
int leftSpaceCnt = numOfSpace - intervalSpaceCnt * (list.size() - 1);
StringBuilder sb = new StringBuilder();
sb.append(list.get(0));
for (int i = 1; i < list.size(); ++i) {
for (int j = 0; j < intervalSpaceCnt; ++j) {
sb.append(" ");
}
sb.append(list.get(i));
}
for (int j = 0; j < leftSpaceCnt; ++j) {
sb.append(" ");
}
return sb.toString();
}
|
9.8

先考虑特殊情况,当 k = n-1 时,通过大小交替的排序方式可以满足题目要求,即 [1,n,2,n-1,3,n-2,4, …]
故想到,可以将 1~n-k 先按顺序排列,剩 k 个数大小交替排列,即 [1, 2, …, n-k, n, n-k+1, n-1, n-k+2,…]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public int[] constructArray(int n, int k) {
int[] ans = new int[n];
for (int i = 1; i <= n - k; ++i) {
ans[i-1] = i;
}
int odd = 0;
int even = k - 1;
for (int j = 0; j < k; ++j) {
if (j % 2 == 0) {
ans[n - k + j] = n - odd;
++odd;
} else {
ans[n - k + j] = n - even;
--even;
}
}
return ans;
}
|
9.9

1
2
3
4
5
6
7
8
9
10
11
| public int minOperations(String[] logs) {
int steps = 0;
for (int i = 0; i < logs.length; ++i) {
if (logs[i].equals("./")) {}
else if (logs[i].equals("../")) {
if (steps > 0) --steps;
}
else ++steps;
}
}
|
9.10
标签:深度搜索,二叉搜索树
思路:根据二叉搜索树的性质,有以下情况
- 若某一节点的左子节点不在边界范围内,则该节点的左子树都不在边界范围内
- 若某一节点的右子节点不在边界范围内,则该节点的右子树都不在边界范围内
- 若某一节点的左子节点在边界范围内,则该节点的右子树都在边界范围内
- 若某一节点的右子节点在边界范围内,则该节点的左子树都在边界范围内
故可以迭代地将不满足条件的节点从二叉搜索树中剔除
注意:迭代之前需要用类似的方法找到一个满足条件的新的根节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public TreeNode trimBST(TreeNode root, int low, int high) {
while (root != null && (root.val < low || root.val > high)) {
if (root.val < low) { root = root.right; }
else { root = root.left; }
}
if (root == null) { return null; }
TreeNode node = root;
while (node.left != null) {
if (node.left.val < low) { node.left = node.left.right; }
else { node = node.left; }
}
node = root;
while (node.right != null) {
if (node.right.val > high) { node.right = node.right.left; }
else { node = node.right; }
}
return root;
}
|
另附上递归(深度搜索)的代码:
1
2
3
4
5
6
7
8
| public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) { return null; }
if (root.val > high) { return trimBST(root.left, low, high); }
if (root.val < low) { return trimBST(root.right, low, high); }
root.left = trimBST(root.left, low, high);
root.right = return trimBST(root.right, low, high);
return root;
}
|
9.11

标签:贪心,优先队列
思路:每个人应得的报酬根据其工作质量的比例从总报酬中分配,并需要满足不低于最低期望,如①式
记一个工人的最低期望工资与对应工作质量之比为ε,经推导,要使总报酬最低,需要总工作质量相同的情况下使得最大的ε值最小,也即,选定了最大ε值的工人之后,其余工人工作质量之和尽量小
$$
Pay_{i}=\Sigma Pay_{i}×\frac{Quality_{i}}{\Sigma Quality_{i}}≥Wage_{i};①\
\Sigma Pay_{i}≥\Sigma Quality_{i}×\frac{Wage_{i}}{Quality_{i}};②\
\Sigma Pay_{i}≥\Sigma Quality_{i}×\epsilon_{max};③\
$$
具体操作:将工人按照ε值从小到大的排序,并逐个添加到一个以工作质量为比较标准的最大堆中,保证先入堆的工人ε值较小。从第k个工人入堆开始需要计算当前k个人产生的总成本,与已有结果比较取更小者。下一个工人入堆之前,需要将已有的k个工人中工作质量最优的人剔除(最大ε值增加而总工作质量尽量地减小)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public double mincostToHireWorkers(int[] quality, int[] wage, int k) {
int n = wage.length;
List<int[]> worker = new ArrayList<>();
for (int i = 0; i < n; ++i) {
worker.add(new int[]{quality[i], wage[i]});
}
worker.sort((a, b) -> { return a[1] * b[0] - a[0] * b[1]; });
PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> y - x);
double minCost = Double.MAX_VALUE;
int totalQuality = 0;
for (int i = 0; i < k-1; ++i) {
int q = worker.get(i)[0];
totalQuality += q;
pq.offer(q);
}
for (int i = k-1; i < n; ++i) {
int q = worker.get(i)[0];
totalQuality += q;
pq.offer(q);
double ratio = worker.get(i)[1] / (double) q;
minCost = Math.min(minCost, totalQuality * ratio);
totalQuality -= pq.poll();
}
return minCost;
}
|
9.12
思路:排序后遍历比较
具体操作:将数组降序排列,一次遍历,同时满足 ①第k个数大于等于k 且 ② 第k+1个数小于k 则返回k,若不满足条件①则不存在特征值,若不满足条件②则继续遍历
1
2
3
4
5
6
7
8
9
10
11
12
| public int specialArray(int[] nums) {
Integer[] a = Arrays.stream(nums).boxed().toArray(Integer[]::new);
Arrays.sort(a, Collections.reverseOrder());
for (int i = 1; i <= a.length; ++i) {
if (a[i-1] >= i) {
if (i == a.length || a[i] < i) { return i; }
else continue;
}
else return -1;
}
return -1;
}
|
9.13

思路:要使交换后一个 n 位数尽量大,应当在前 k 位已经最大的情况下,将第 k+1 位与第 k+2 到第 n 位中最大且最靠近个位的位进行交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public int maximumSwap(int num) {
List<Integer> intBits = new ArrayList<>();
List<Integer> intBitsInOrder = new ArrayList<>();
int temp = num;
while (temp > 0) {
int intBit = temp % 10;
intBits.add(intBit);
intBitsInOrder.add(intBit);
temp /= 10;
}
intBitsInOrder.sort(Comparator.naturalOrder());
int n = intBits.size();
int indexToChange = -1;
for (int i = n-1; i >= 0; --i) {
if (intBits.get(i) == intBitsInOrder.get(i)) continue;
indexToChange = i;
break;
}
if (indexToChange == -1) return num;
for (int i = 0; i < indexToChange; ++i) {
if (intBits.get(i) == intBitsInOrder.get(indexToChange)) {
int maxSwap = 0;
for (int j = n-1; j >= 0; --j) {
int index = j;
if (index == indexToChange) index = i;
else if (index == i) index = indexToChange;
maxSwap = maxSwap * 10 + intBits.get(index);
}
return maxSwap;
}
}
return -1;
}
|
9.14
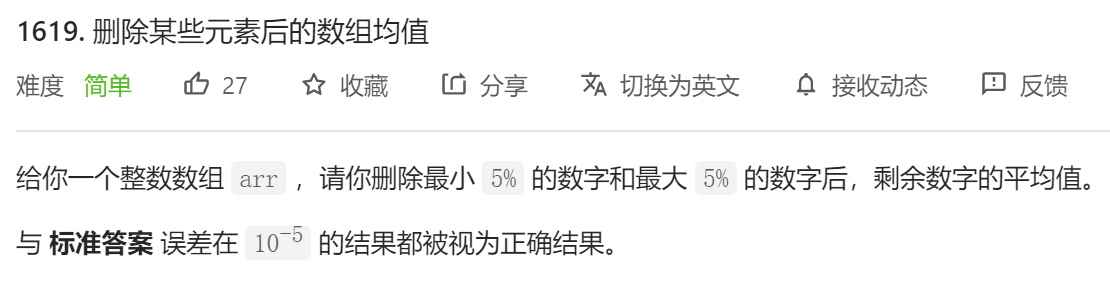
傻子题不想动脑子了…
1
2
3
4
5
6
7
8
9
10
| public double trimMean(int[] arr) {
Arrays.sort(arr);
int len = arr.length;
int n = len * 5 / 100;
double sum = 0.0;
for (int i = n; i < len-n; ++i) {
sum += arr[i];
}
return sum / (len - 2*n);
}
|
9.15
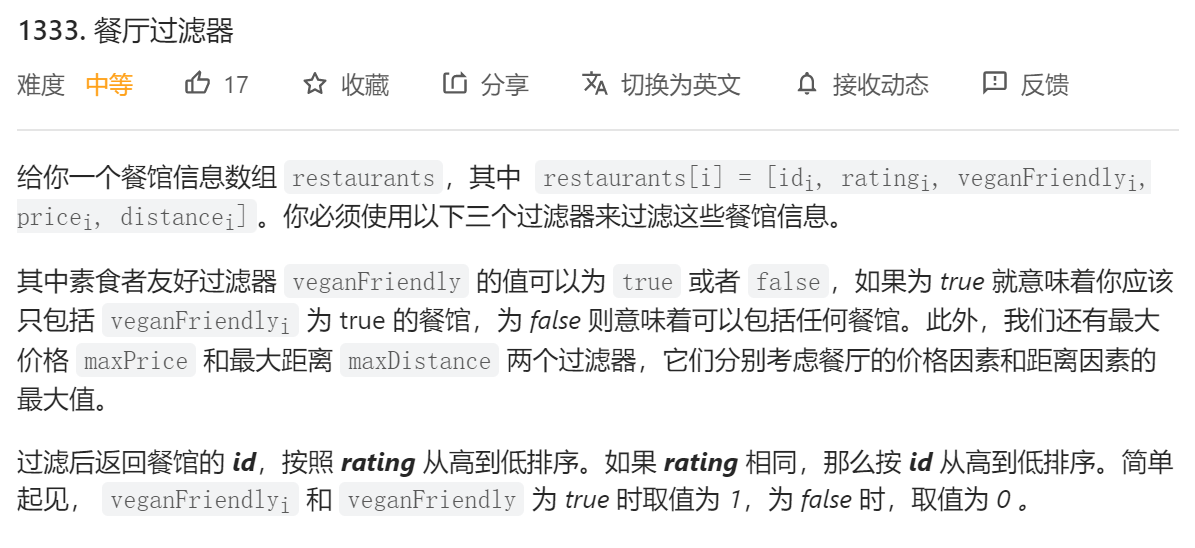
思路:过滤+排序,可以使用 Java8 中的 Stream 类型来清晰地处理
具体实现:filter 过滤流中的元素;sorted 对流中的元素排序;map 对流中的元素进行映射
1
2
3
4
5
6
7
8
9
| public List<Integer> filterRestaurants(int[][] restaurants, int veganFriendly, int maxPrice, int maxDistance) {
return Arrays.stream(restaurants)
.filter(e -> veganFriendly == 0 || veganFriendly == 1 && e[2] == 1)
.filter(e -> e[3] <= maxPrice)
.filter(e -> e[4] <= maxDistance)
.sorted((a, b) -> a[1] != b[1] ? b[1] - a[1] : b[0] - a[0])
.map(e -> e[0])
.toList();
}
|
9.16
太难了做不出来,答案也看不懂,咕咕咕~
9.17
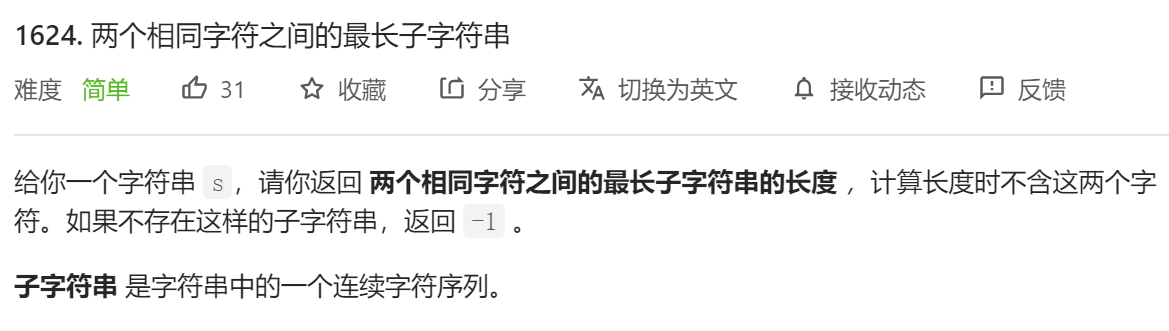
简单题美滋滋~
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int maxLengthBetweenEqualCharacters(String s) {
Set<Character> letters = new HashSet<>();
for (int i = 0; i < s.length(); ++i) {
letters.add(s.charAt(i));
}
int maxLen = -1;
for (char ch : letters) {
int i = s.indexOf(ch);
int j = s.lastIndexOf(ch);
maxLen = Math.max(j-i-1, maxLen);
}
return maxLen;
}
|
9.18
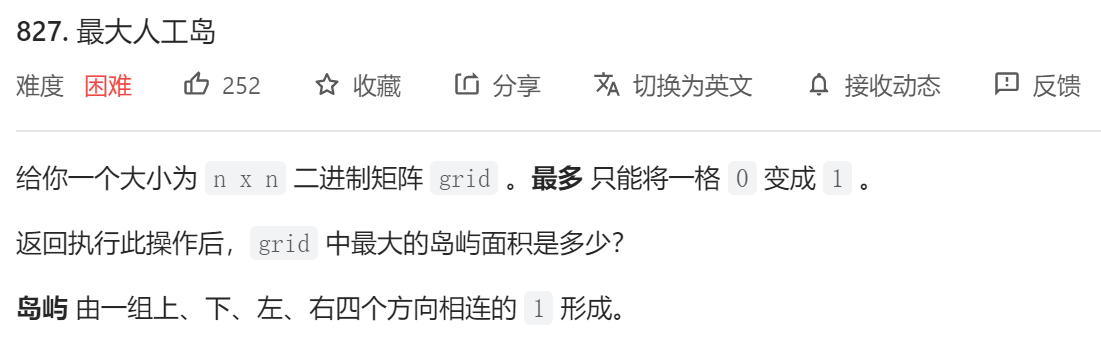
9.19

1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int[] frequencySort(int[] nums) {
Map<Integer, Integer> freqMap = new HashMap<>();
for (int i = 0; i < nums.length; ++i) {
if (freqMap.containsKey(nums[i])) {
freqMap.replace(nums[i], freqMap.get(nums[i])+1);
} else {
freqMap.put(nums[i], 1);
}
}
Integer[] temp = Arrays.stream(nums).boxed().toArray(Integer[]::new);
Arrays.sort(temp, (x,y) ->
freqMap.get(x) == freqMap.get(y) ? y-x : freqMap.get(x)-freqMap.get(y));
return Arrays.stream(temp).mapToInt(Integer::valueOf).toArray();
}
|
9.20
不会做… 抄的网上的答案…
思路:递归地按照从大到小的顺序把数组中的数放入k个槽位中,使得每个槽位中数的和小于等于目标和
剪枝策略:若 cur[j] 与 cur[j-1] 相等,意味着在 cur[j-1] 时已经完成了搜索,可跳过当前的搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public boolean canPartitionKSubsets(int[] nums, int k) {
int sum = Arrays.stream(nums).sum();
if (sum % k != 0) { return false; }
int subSum = sum / k;
Arrays.sort(nums);
int[] curSum = new int[k];
return dfs(nums, curSum, subSum, nums.length-1);
}
private boolean dfs(int[] nums, int[] curSum, int subSum, int i) {
if (i < 0) { return true; }
for (int j = 0; j < curSum.length; ++j) {
if (j > 0 && curSum[j] == curSum[j-1]) { continue; }
curSum[j] += nums[i];
if (curSum[j] <= subSum && dfs(nums, curSum, subSum, i-1)) { return true; }
curSum[j] -= nums[i];
}
return false;
}
|
9.21
咕咕咕~
9.22
???
9.23

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
| class MyLinkedList {
public class Node {
int val;
Node prev;
Node next;
Node(int val) {
this.val = val;
this.next = null;
this.prev = null;
}
}
Node head;
Node tail;
int length;
public MyLinkedList() {
this.length = 0;
this.head = new Node(0);
this.tail = new Node(0);
this.head.prev = null;
this.head.next = this.tail;
this.tail.prev = this.head;
this.tail.next = null;
}
public int get(int index) {
if (index < 0 || index >= this.length) {
return -1;
}
Node curr = head;
for (int i = 0; i <= index; ++i) {
curr = curr.next;
}
return curr.val;
}
public void addAtHead(int val) {
Node node = new Node(val);
node.next = this.head.next;
this.head.next.prev = node;
node.prev = this.head;
this.head.next = node;
++this.length;
}
public void addAtTail(int val) {
Node node = new Node(val);
node.prev = this.tail.prev;
this.tail.prev.next = node;
node.next = this.tail;
this.tail.prev = node;
++this.length;
}
public void addAtIndex(int index, int val) {
if (index <= 0) {
addAtHead(val);
} else if (index == this.length) {
addAtTail(val);
} else if (index > 0 && index < this.length) {
Node node = new Node(val);
Node curr = this.head;
for (int i = 0; i <= index; ++i) {
curr = curr.next;
}
Node prev = curr.prev;
prev.next = node;
node.prev = prev;
node.next = curr;
curr.prev = node;
++this.length;
}
}
public void deleteAtIndex(int index) {
if (index >= 0 && index < this.length) {
Node curr = this.head;
for (int i = 0; i <= index; ++i) {
curr = curr.next;
}
Node prev = curr.prev;
Node next = curr.next;
prev.next = next;
next.prev = prev;
--this.length;
}
}
}
|
Author:
Yoson Ling
License:
Copyright (c) 2019 CC-BY-NC-4.0 LICENSE















